实验内容
基于DTW算法实现单个词的语音识别
实验思路
MFCC
根据上课所学知识,对于单个词的语音进行识别,首先需要将输入的音频信号转化为语音特征MFCC、即梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC),而MFCC的生成流程如下图所示: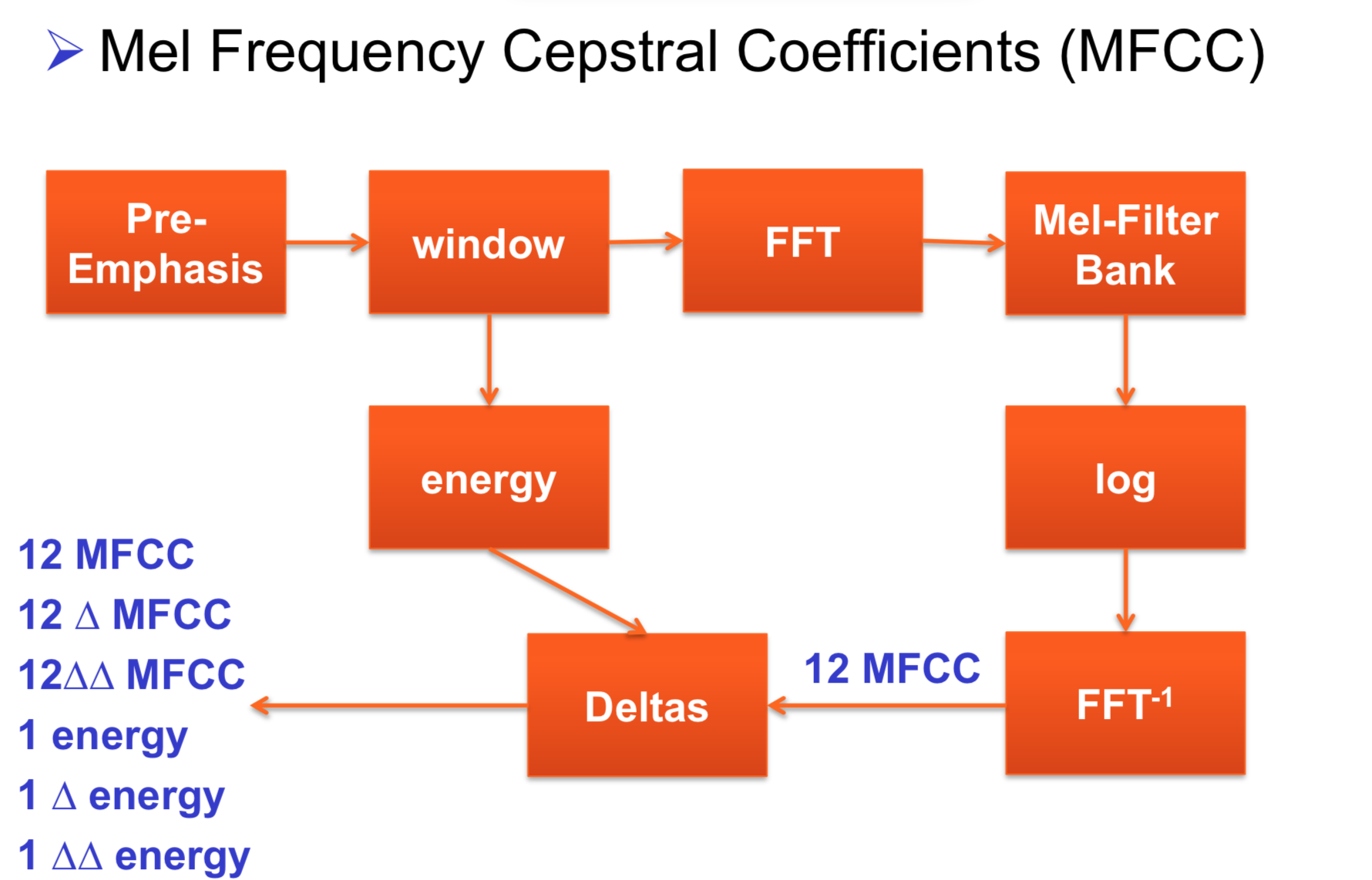
为了识别待识别语音,我们首先应该得到一些模版特征(template MFCC),得到template mfcc后,对于每一条输入进来的待测试音频,将其与模版挨个匹配即可,其最终的分属类别即属于最相似的模版类属。
DTW
DTW,即Dynamic Time Warping、动态时间规整算法,为MFCC的匹配提供了一个最基础的方法,其应用思路是:对于表述同样内容的两端音频,由于说话人音色、语速的不同,从而造成了相同的音素在发音时占用着不同的时常,而这些音素在比较时又被务必分在同一类别之下,所以就有了将DTW应用至此的思路。
DTW的过程可表示如下: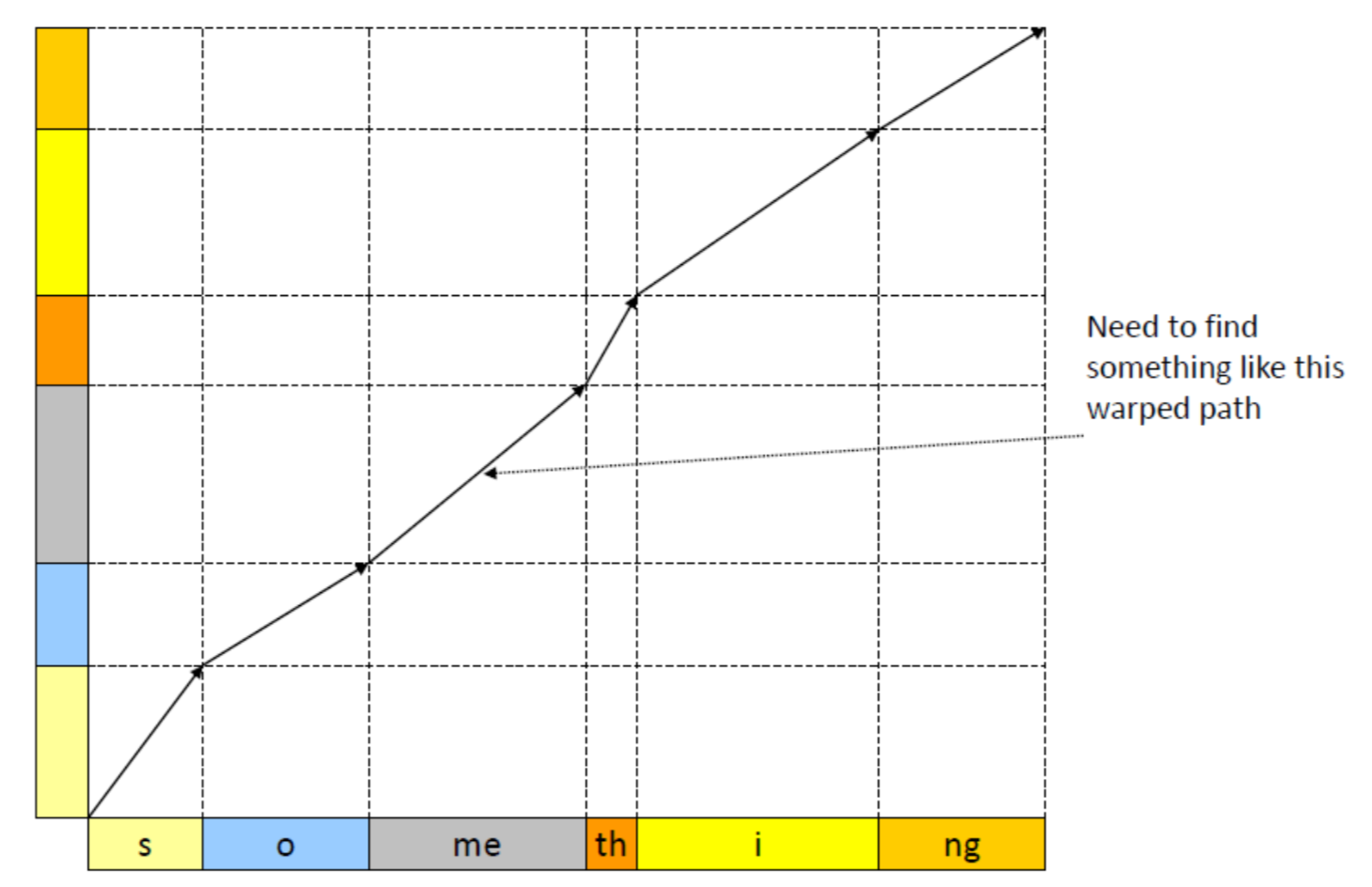
所以现在我们需要定义上图中的wraped path
对wraped path的定义有以下两种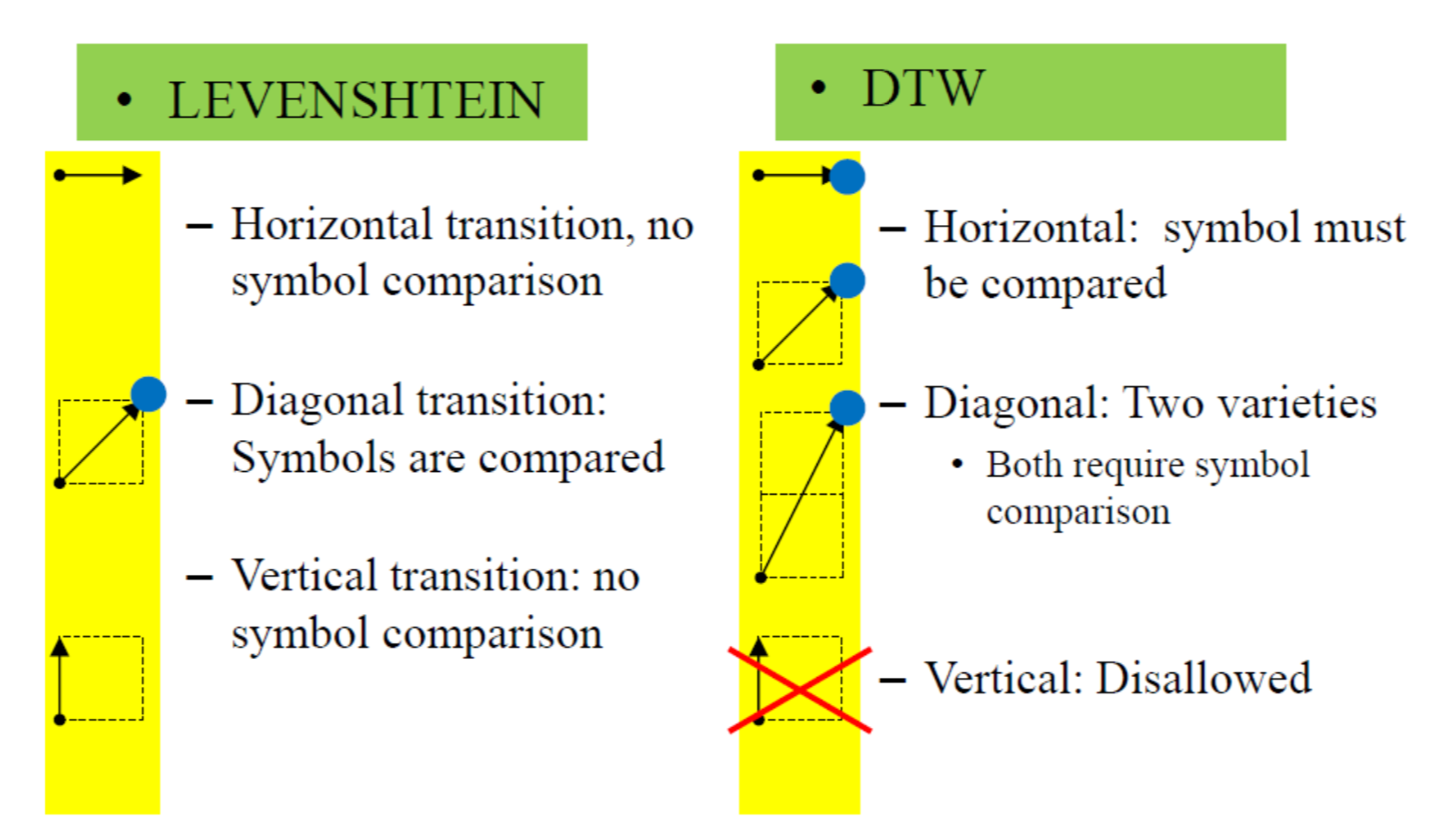
两者的主要区别在于:Vertical match是否被允许,即是否允许跳过当前的symbol或必须匹配当前的symbol
显然,DTW的求解过程是一个动态规划的思路,所以对于以上两种思路,DP过程可被分别表示如下:
- LEVENSHTEIN:
$$
cost_{i,j} = dist_{i,j} + min(cost_{i,j-1}, cost_{i-1,j}, cost_{i-1,j-1})
\\ where \qquad cost_{0,0} = dist_{0,0}, i > 0, j > 0
$$ - DTW:
$$
cost_{i,j} = dist_{i,j} + min(cost_{i,j-1}, cost_{i-1,j-1}, cost_{i-2,j-1})
\\ where \qquad cost_{0,0} = dist_{0,0}, i > 1, j > 0
$$
实验过程
有了以上思路后,接下来编写程序实现上述思路:
实验环境
- 系统:Mac OS X
- 语言:python3.6.5
- requirements:
- numpy
- scipy.io.wavfile: 用于wav数据读取
- python_speech_features.base: 用于生成MFCC特征
- matplotlib
项目结构
为了保证泛用性,这里使用面向对象的思想来实现单个词语音识别,定义为Digit_Voice_Rec类:
| 方法 | 说明 |
|---|---|
| __init__ | 实现类的初始化以及公共变量的赋值 |
| get_input | 读取wav文件,返回rate及Amplitude |
| get_mfcc | 接收get_input的读入数据,返回对应的MFCC特征 |
| gather_mfcc | 整合将所有的数据集,返回总的MFCC列表 |
| get_template | 取出当前代表当前类别的模版MFCC |
| DTW | 基于DTW的DP实现 |
| LEVENSHTEIN | 基于LEVENSHTEIN的DP实现 |
| run_Voice_rec | 测试算法的acc及表现 |
运行步骤
项目的运行逻辑及数据流如下图所示: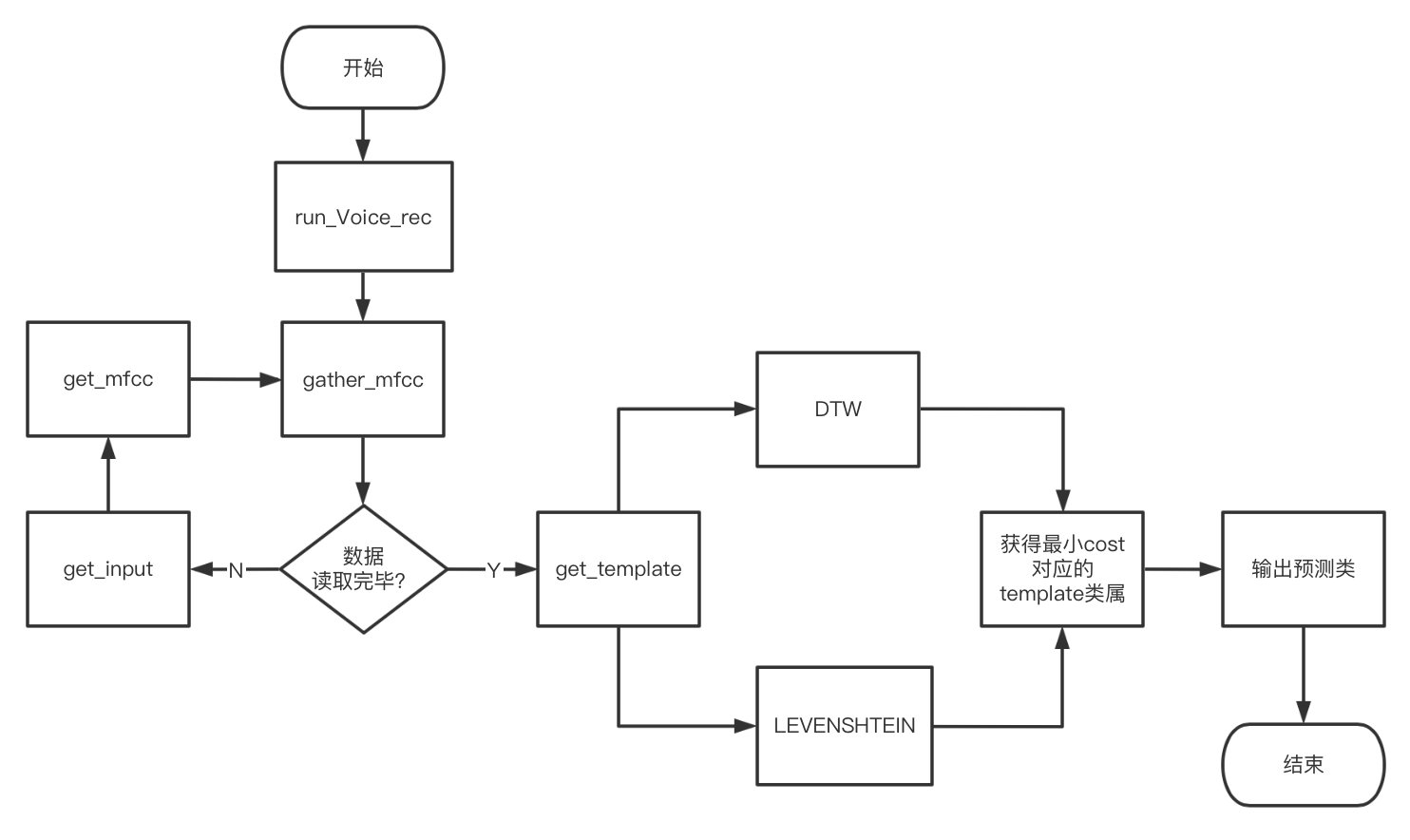
实验结果
数据集
本次试验的数据集来源于github上的公开资源,每个数字5条语音数据,有0~9共50条数据
英文数字语音
语谱图如图所示: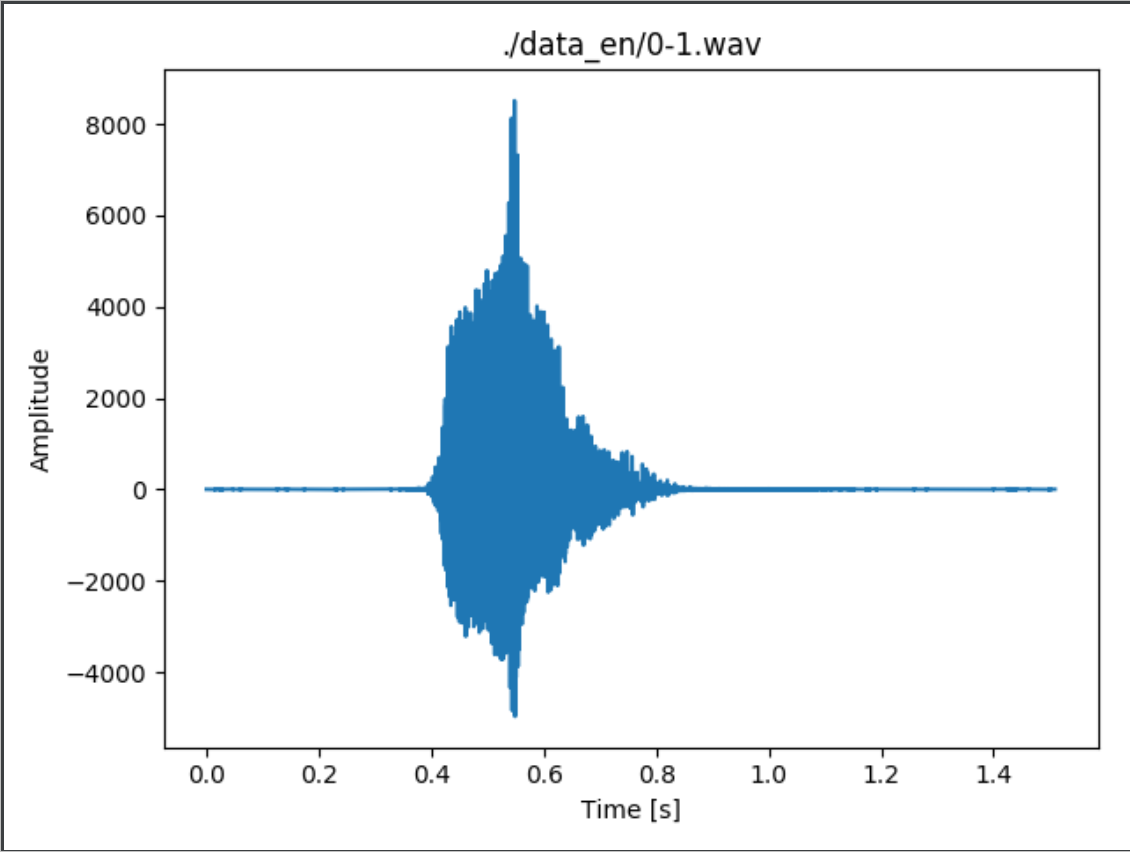
实验结果
DTW
1 | /Library/Frameworks/Python.framework/Versions/3.6/bin/python3.6 |
LEVENSHTEIN
1 | /Library/Frameworks/Python.framework/Versions/3.6/bin/python3.6 |
可以看到,在此数据集下,使用LEVENSHTEIN和DTW的区别并不大。
改进
DTW相较于LEVENSHTEIN的改进只是在模版匹配中删改了vertical的对齐动作,对于进一步的改进,考虑在模版匹配中增加新的改进方法。
上面的实验都是基于单模版进行的匹配,单模版虽然执行速度快,但却无法保证选出的单模版是一个较为“整齐”的MFCC,所以改进时可以考虑使用多个MFCC构造模版,从一定程度上消减了因偶然性引起的匹配误差。
我们假定在以下的多模版匹配中每个类别对应的候选模版数目均有$t_k$个,每个类别下的$t_k$可以相同也可不同。
多模版均值匹配
该方法的思路是:对于每个类别下多个候选模版,测试数据$MFCC_i$去和每一个模版$template\_MFCC_j \quad j \in t_k$执行DTW对齐操作,并获得对应的代价$cost_j$,最终$MFCC_i$属于该类的总代价便是各个模版下对应代价的加权平均$cost_i = \sum_{j \in t_k} p_j*cost_j$
这里的$p_j$可以由一些先验来设定,比如认为观察到一些模版数据不能满足该类别下的对齐需求,即对应的$cost$总是非常大,那么就可以人为的降权,一般而言在时间中,总是使用平均权重。
1 | predict digit: 0, true label: 0 |
多模版全局最小值匹配
均值匹配提供了一个初步的思路,即同时利用多个模版数据来进行匹配,该方法虽然能在一定程度上消除在单模版匹配中碰到的随机选择模版上的误差,但是如果我们选择的$t_k$个模版有$t_k-1$个都是“不好的”,那么在没有先验知识时,使用平均权重会带来很大的误差。
考虑到整个匹配过程的核心思想是:匹配所得类别即最小代价对应的模版类,所以在使用多模版时,我们可以放弃平均累计的思想,只要在该类中得到了一个足够小的$cost_{min}$,且别的所有模版中均未有高过$cost_min$的值,就认为该$MFCC_i$属于$cost_{min}$对应的类
这样子改进的好处是,不仅可以消除单个template选取的偶然误差,还能够在没有先验知识时最大程度上消除由多个“不好的”模版带来的混合误差。
实验结果如下($t_k=3$):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22/Library/Frameworks/Python.framework/Versions/3.6/bin/python3.6
predict digit: 0, true label: 0
predict digit: 0, true label: 0
predict digit: 1, true label: 1
predict digit: 1, true label: 1
predict digit: 2, true label: 2
predict digit: 2, true label: 2
predict digit: 3, true label: 3
predict digit: 3, true label: 3
predict digit: 4, true label: 4
predict digit: 4, true label: 4
predict digit: 5, true label: 5
predict digit: 1, true label: 5
predict digit: 6, true label: 6
predict digit: 6, true label: 6
predict digit: 7, true label: 7
predict digit: 7, true label: 7
predict digit: 8, true label: 8
predict digit: 8, true label: 8
predict digit: 9, true label: 9
predict digit: 9, true label: 9
Acc: 0.95
结果分析
从实验结果来看,均值匹配如我们上述分析,其在没有先验来确定$p_j$时,单使用平均权重并不能起到一个很好的提升效用,从另一个角度看,全局最小的确是一个可信赖的方法,除了匹配速度较慢(因为要对比所有模版),效果还是可观的。
代码附录
1 | # -*- coding: utf-8 -*- |

