这一部分讲一下TD,也就是时序差分学习。
TD(0)算法
在使用蒙特卡罗方法时,对价值函数的更新采用如下方法:
$$
V(S_t) = V(S_t) + \alpha[G_t - V(S_t)]
$$
也就是说,要实现状态价值/动作价值的更新必须要等到一幕结束,因为只有一幕结束后,回报Gt才可知。
时序差分学习加速了价值的更新,其直接使用下一个时刻的价值估计值以及此刻观察到的收益来对价值函数进行更新:
$$
V(S_t) = V(S_t) + \alpha[R_t + \gamma V(S_{t+1}) - V(S_t)]
$$
这种方法被称为TD(0)。
TD算法结合了MC采样方法和DP的自举法,对算法描述如下:
对每一幕循环:
初始化S
对幕中的每一步循环:A = 在状态S下根据策略π作出的决策动作
执行动作A,观察到R与S’
V(S) = V(S) + α[R + γV(S’) - V(S)]
S = S’
在多数情况下,TD算法的表现均优于DP和MC算法:
- 相比DP:不需要环境模型,即描述收益和下一状态联合概率分布的模型。
- 相比MC:自然的运用了一种在线、完全地震的方法来实现。价值更新只需要等到下一个时刻即可。
接下来我们使用TD方法来解决实际的控制问题。
在评估和预测的部分使用TD方法,按照惯例,需要在explore和exploit之间做出权衡,方法被划分为on-policy与off-policy两种。
Sarsa
算法由来
Sarsa是on-plocy下的TD。
其需要学习的是动作价值函数q(s,a)而不是状态价值函数V(s)。
Sarsa对动作价值的更新方法如下:
$$
Q(S_t,A_t) = Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)]
$$
可以看到,对于一次状态更新,可以用一个五元组来表示:$(S_t,A_t,R_{t+a},S_{t+1},A_{t+1})$,这也是Sarsa算法名字的由来。
算法描述
Sarsa的算法流程描述如下:
对每一幕循环:
初始化S
使用从Q中得到的策略(如ε-greedy),在S处选取A
对幕中的每一步循环:执行动作A,观察到R与S’
使用从Q中得到的策略(如ε-greedy),在S’处选取A’
Q(S,A) = Q(S,A) + α[R + γQ(S’,A’) - Q(S,A)]
S = S’
A = A’
下面通过一个实际的问题来深入理解Sarsa的实现:
有风的网格世界
问题背景
背景为书中的例6.5,以之前介绍过的网格世界为背景,加入了环境干扰,即风。
在有风的区域内,动作的执行会收到风的干扰。
超参数
超参数如下:
规定了网格边界、风带来的影响、动作空间、ε-greedy的ε参数、Sarsa的固定步长、每时刻收益、起点终点坐标:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27# world height
WORLD_HEIGHT = 7
# world width
WORLD_WIDTH = 10
# wind strength for each column
WIND = [0, 0, 0, 1, 1, 1, 2, 2, 1, 0]
# possible actions
ACTION_UP = 0
ACTION_DOWN = 1
ACTION_LEFT = 2
ACTION_RIGHT = 3
# probability for exploration
EPSILON = 0.1
# Sarsa step size
ALPHA = 0.5
# reward for each step
REWARD = -1.0
START = [3, 0]
GOAL = [3, 7]
ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]
S->S’
状态变化的实现如下,主要由动作和风力影响共同实现1
2
3
4
5
6
7
8
9
10
11
12def step(state, action):
i, j = state
if action == ACTION_UP:
return [max(i - 1 - WIND[j], 0), j]
elif action == ACTION_DOWN:
return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
elif action == ACTION_LEFT:
return [max(i - WIND[j], 0), max(j - 1, 0)]
elif action == ACTION_RIGHT:
return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
else:
assert False
动作价值估计
根据上面给出的Sarsa算法描述,对每一幕中的动作价值估计,通过代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42def episode(q_value):
# track the total time steps in this episode
time = 0
# initialize state
state = START
# choose an action based on epsilon-greedy algorithm
if np.random.binomial(1, EPSILON) == 1:
# ε的概率去随机选取(explore)
action = np.random.choice(ACTIONS)
else:
# 1-ε的概率根据动作价值选取(exploit):
# 返回四个动作对应的价值
values_ = q_value[state[0], state[1], :]
# 从最大值的
# action_为枚举values_时对应的下标:0~3
action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# keep going until get to the goal state
while state != GOAL:
# 执行动作A,观察到新状态S'
# reward固定,不到终止状态都为-1
next_state = step(state, action)
# 根据ε-greedy选取动作A'
if np.random.binomial(1, EPSILON) == 1:
next_action = np.random.choice(ACTIONS)
else:
values_ = q_value[next_state[0], next_state[1], :]
next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# Sarsa update
# Q(S,A) = Q(S,A) + α[R + γQ(S',A') - Q(S,A)]
q_value[state[0], state[1], action] += \
ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
q_value[state[0], state[1], action])
# S=S'
state = next_state
# A=A'
action = next_action
time += 1
return time
这里的on-policy可以理解为:在S处选取A的策略 与 在更新动作价值Q(S,A)时在S’处选取A’的策略相同(均为ε-greedy)
实验结果
实验结果如下,可以看到随着时间的推移,目标达成的越来越快: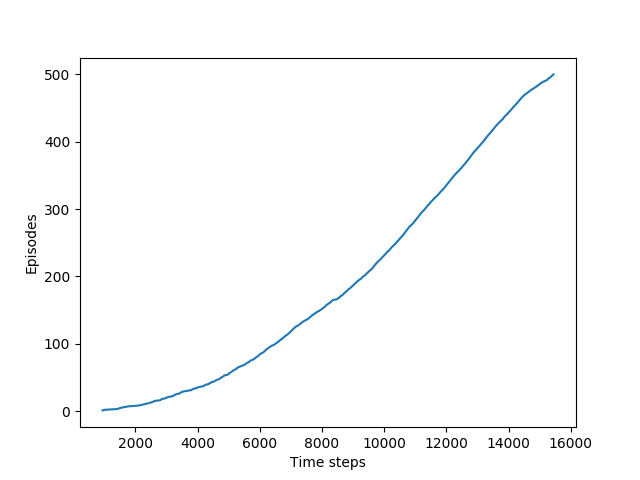
Sarsa给出的最优策略为:
该实验显示出了Sarsa优于MC方法的另一面:
在MC方法中,如果发现某个策略使agent停留在同一个状态内,那么下一幕任务就永远不会开始;
但Sarsa这样一步一步的学习方法则没有这个问题,因为其在当前幕运行过程中就能很快的学到当前的策略,如果不够好,然后就会切换到其他的策略。
参考文献
[1] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

