上一节介绍MC算法时,为了克服试探性出发这一强假设,rf提出了通过On-Policy和Off-Policy两种持续采样的方法。
在Off-Policy中,为了通过行动策略b观察到的多幕采样序列的平均回报来预测状态价值$v_\pi(s)$,需要根据重要度采样比来调整回报值、并对结果进行平均,根据调整平均方式的不同,又引申出了两种方法:
普通重要度采样和加权重要度采样。
从数学的角度来看:
普通重要度采样:
无偏估计
方差无界加权重要度采样
有偏估计(偏差逐渐收敛到0)
假设回报值有界,即使重要度采样比方差无界,方差仍然能收敛到0
下面我们从一个简单的模型入手来讨论普通重要度采样的无穷方差问题。
问题背景
状态转移概率以及收益如图所示: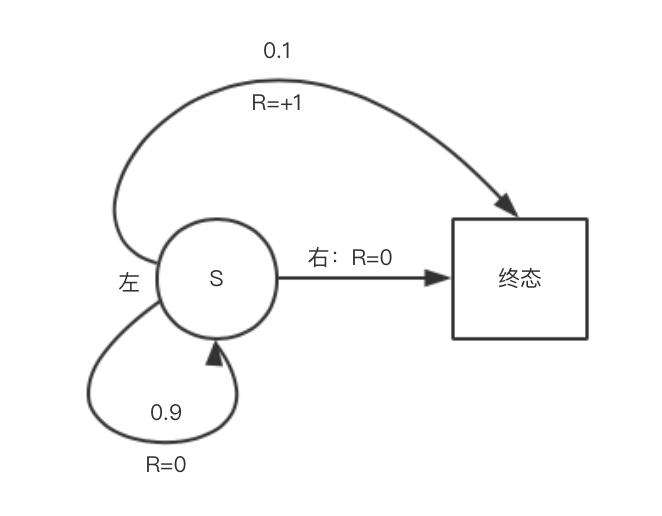
这里指定目标策略$\pi(向左|s)=1$,行动策略$b(向左|s)=1/2$.
在目标策略下,总是采取向左的行动(因为只有向左才有收益+1);在行动策略下,等概率执行向左向右行动。
代码实现
超参数
本题题量较小,涉及到的超参数也不多,超参数仅指定好想左/右的动作即可:1
2ACTION_BACK = 0 # left
ACTION_END = 1 # right
策略
模型背景中给出了行为策略和目标策略的定义,代码实现如下:1
2
3
4
5
6
7# behavior policy:左右各为0.5
def behavior_policy():
return np.random.binomial(1, 0.5)
# target policy:只向左走
def target_policy():
return ACTION_BACK
一幕动作
每一幕中的动作:从s开始选择向左或向右,直到到达终态结束为止。1
2
3
4
5
6
7
8
9
10
11
12
13# one turn
def play():
# track the action for importance ratio
trajectory = []
while True:
action = behavior_policy()
trajectory.append(action)
# 直接向右:结束
if action == ACTION_END:
return 0, trajectory
# 向左0.9概率回到自身失败,即向左0.1概率到达终态
if np.random.binomial(1, 0.9) == 0:
return 1, trajectory
根据重要度采样调和回报
这里讨论基于普通重要度采样的回报:1
2
3
4
5
6
7
8
9
10rewards = []
for episode in range(0, episodes):
reward, trajectory = play()
if trajectory[-1] == ACTION_END:
rho = 0
else:
rho = 1.0 / pow(0.5, len(trajectory))
rewards.append(rho * reward)
rewards = np.add.accumulate(rewards)
estimations = np.asarray(rewards) / np.arange(1, episodes + 1)
回到问题背景中可以看到,行动策略b是一个(n,0.5)的二项分布,在计算时仅需计算0.5的连乘即可。
由于目标策略π下的动作总是向左,即一旦trajectory中出现了向右的动作(向右即进入终态结束,所以只可能出现在最后一个),那意味着分子中将会出现一项$π(a|s)=0$,随机导致整个重要度采样比归0.
实验结果
结果如图所示,可以看到:在独立训练10轮,每轮100000幕的情况下,普通重要度采样能让难以收敛到1(在折扣率为1时,持续向左一定能获得收益+1)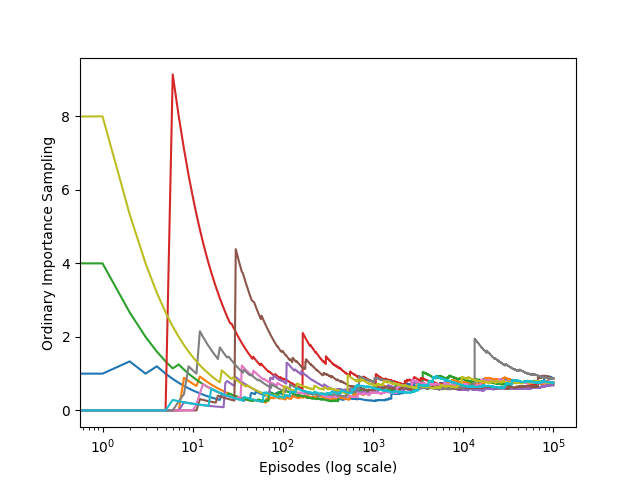
对比实验
为了与加权重要度采样对比,我对代码做了一点修改:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19for run in range(runs):
rewards = []
# 记录采样比序列
rho1 = []
for episode in range(0, episodes):
reward, trajectory = play()
if trajectory[-1] == ACTION_END:
rho = 0
else:
rho = 1.0 / pow(0.5, len(trajectory))
rho1.append(rho)
rewards.append(rho * reward)
rewards = np.add.accumulate(rewards)
# 计算加权重要度采样
rho1 = np.add.accumulate(rho1)
with np.errstate(invalid='ignore'):
e1 = np.where(rho1!=0, np.asarray(rewards)/rho1, 0)
plt.plot(e1)
结果如图: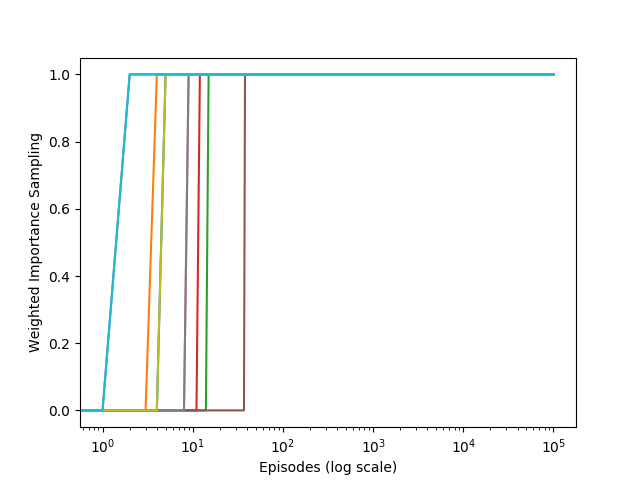
可以看到:加权重要度采样方法仅仅在不到100轮的情况下就稳定的收敛到了正确回报+1!
参考文献
[1] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

