这里我们开始讨论利用蒙特卡罗方法寻找最优策略。
实话说,MC算法比起前几章来说难度提升了一个档次,但其又是rf后续学习的基础,所以不可懈怠。
本篇以游戏:21点为例,分别讲述蒙特卡洛方法依托于以下三个算法的实现:
- 试探性出发 Monte Carlo with Exploring Starts
- 同轨策略 Monte Carlo Sample with On-Policy
- 离轨策略 Monte Carlo Sample with Off-Policy
蒙特卡罗方法要点
与DP不同,MC算法仅仅需要经验(通过采样获得的数据),而不像DP需要完备的环境知识(如租车还车分布等)去遍历状态空间。
MC算法通过平均样本的回报来解决强化学习的问题,价值估计以及策略改进在整个episode结束时进行,这意味着MC算法是逐幕改进的(offline),而非在每个时刻都有改进(online)。
在rf中,“蒙特卡洛”特指对完整回报取平均的算法。
游戏介绍
21点游戏,原译为blackjack。
扑克牌A,2~10、JQK分别代表[1或11,2~10、10],Ace牌可看作1或11。
玩家和庄家开始先发两张牌,庄家明牌一张,若玩家开始两张牌之和小于12则可持续补牌。
游戏开始:
- 玩家根据一定策略先持续要牌,若为和为21则直接获胜,超过21则认输,适当后停牌
- 玩家停牌后庄家根据一定策略要牌,若为和为21则直接获胜,超过21则认输,适当后停牌
- 两人停牌后比较手牌和大小,大的获胜。
超参设计
同样的,首先来设计问题建模所需要的超参数。
动作空间:
1
2
3
4# actions: hit or stand
ACTION_HIT = 0 # 要牌
ACTION_STAND = 1 # 停牌
ACTIONS = [ACTION_HIT, ACTION_STAND]玩家策略
根据题干要求:玩家在手牌和小于20时持续要牌1
2
3
4
5
6# 玩家的策略:12~19:要牌、20~21:停牌
POLICY_PLAYER = np.zeros(22, dtype=np.int)
for i in range(12, 20):
POLICY_PLAYER[i] = ACTION_HIT
POLICY_PLAYER[20] = ACTION_STAND
POLICY_PLAYER[21] = ACTION_STAND庄家策略
根据题干要求:庄家在手牌和小于17时持续要牌1
2
3
4
5
6# 庄家的策略:小于17时要牌、17~21时停牌
POLICY_DEALER = np.zeros(22)
for i in range(12, 17):
POLICY_DEALER[i] = ACTION_HIT
for i in range(17, 22):
POLICY_DEALER[i] = ACTION_STAND扑克生成
随机生成扑克数值1~131
2
3
4
5
6# 随机生成牌(1~13)->(1~10)
# card的范围【1~10】
def get_card():
card = np.random.randint(1, 14)
card = min(card, 10)
return card扑克价值
随机生成扑克数值2~11,Ace先默认为111
2
3# card_value的范围【2~11】
def card_value(card_id):
return 11 if card_id == 1 else card_id
游戏过程建模
游戏共有:输、赢、和三个结果,其收益分别定义为+1、-1、0.
MC算法由于不知晓环境模型,所以其核心在于求取动作价值Q而非状态价值V。
这并不是一个简单的事情,我们通过如下过程建模来求取动作价值Q:
参数设定
输入值:1
def play(policy_player, initial_state=None, initial_action=None):
- policy_player:即玩家策略,由于庄家策略是固定的POLICY_DEALER,所以可操作的策略为玩家策略。这里可以选用固定的目标策略POLICY_PLAYER,也可以自定义行动策略b来保证对状态空间的探索。
- initial_state:【是否将Ace用作11,玩家手牌和,庄家明牌】三元组【usable_ace_player, player_sum, dealer_card1】。
- initial_action:用作玩家的初试动作。
玩家参数:
- player_sum:玩家手牌和。
- usable_ace_player:是否将Ace用作11。
庄家参数:
- dealer_card1:明牌。
- dealer_card2:初始发牌的第二张。
- usable_ace_dealer:是否将Ace用作11。
返回值:1
return state, reward, player_trajectory
- state:游戏初始状态的三元组[usable_ace_player, player_sum, dealer_card1]
- reward:【胜、平、负】分别收益【1,0,-1】
- player_trajectory:【(是否有ace,玩家手牌之和,地主明牌),行为】轨迹,用于价值估计/策略评估/改进。
发牌
根据游戏规则,玩家和庄家初始发牌数为2。
但玩家在两张手牌之和小于12时会继续要牌,实现代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25# 随机初始化
if initial_state is None:
# 在最开始,即默认有两张手牌
# 如果玩家手中的点数小于11那么必然会要牌直到超过11点
while player_sum < 12:
card = get_card() # card_id【1~10】
player_sum += card_value(card) #card_value【2~11】
# 超过21时,可能有两张Ace
if player_sum > 21:
# 超过21时只有22这一种情况,因为手牌和超过11后不会继续要牌
# 即指有可能为11+x,而x最大为11
assert player_sum == 22
# 所以手牌和为22时必然有一张Ace,此时将其用作1
player_sum -= 10
else: # 要完牌后手牌之和还小于等于21,如果其是ace则认为ace被用作11
usable_ace_player |= (1 == card)
# 初始化庄家牌
dealer_card1 = get_card() # 亮牌
dealer_card2 = get_card()
# 给定初始化
else:
usable_ace_player, player_sum, dealer_card1 = initial_state
dealer_card2 = get_card()
打牌
玩家
玩家行为如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 # player's turn
while True:
# 第一步动作由给定值初始化
if initial_action is not None:
action = initial_action
initial_action = None
# 若没有指定动作或此时不是第一步,则动作由输入玩家策略policy_player决定
else:
# 动作包括【要牌,停牌】
action = policy_player(usable_ace_player, player_sum, dealer_card1)
# 追溯玩家的轨迹,服务重要采样
# 轨迹包括【(是否有ace,玩家手牌之和,地主明牌),行为】
player_trajectory.append([(usable_ace_player, player_sum, dealer_card1), action])
# 停牌
if action == ACTION_STAND:
break
# 否则即为继续要牌
card = get_card()
# 单独使用usable_ace_player不足以区分手牌中用作11的Ace数量,需额外使用ace_count变量
ace_count = int(usable_ace_player)
# 先将ace当作11用
if card == 1:
ace_count += 1
player_sum += card_value(card)
# 如果手牌和超过了21且ace可用,则将ace_count中的一张ace用作1
while player_sum > 21 and ace_count:
player_sum -= 10
ace_count -= 1
# 如果所有ace用作1后仍然大于21,则玩家爆牌,返回收益-1
if player_sum > 21:
return state, -1, player_trajectory
assert player_sum <= 21
# ace_count此时代表用作11的ace,此时只有【0、1】两种可能
usable_ace_player = (ace_count == 1)
庄家
庄家行为如下:除要/停牌策略外,其余同上1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22# dealer's turn
while True:
# 庄家策略为固定策略,由POLICY_DEALER决定
action = POLICY_DEALER[dealer_sum]
# 停牌
if action == ACTION_STAND:
break
# if hit, get a new card
new_card = get_card()
ace_count = int(usable_ace_dealer)
if new_card == 1:
ace_count += 1
dealer_sum += card_value(new_card)
while dealer_sum > 21 and ace_count:
dealer_sum -= 10
ace_count -= 1
# 庄家爆牌
if dealer_sum > 21:
return state, 1, player_trajectory
usable_ace_dealer = (ace_count == 1)
结束
当二人均停牌时,取牌结束,比较二者大小即可分出胜负:1
2
3
4
5
6
7
8# 在双方未爆牌情况下比较结果
assert player_sum <= 21 and dealer_sum <= 21
if player_sum > dealer_sum:
return state, 1, player_trajectory
elif player_sum == dealer_sum:
return state, 0, player_trajectory
else:
return state, -1, player_trajectory
试探性出发 Exploring Starts
蒙特卡罗算法由于不知晓完整的环境模型,且其探索空间为行动策略下的幕序列,所以为了保证算法收敛,模型做了两个比较强的假设:
- 试探性出发
- 进行策略评估时有无限多的episode下的样本序列可供试探
这里首先讨论试探性出发。
所谓试探性出发,即:保证所有的“状态,动作”二元组均有非0的概率被选为起点
需要注意的是,策略改进的方法在当前价值函数上贪心的选取动作,由于我们有动作价值函数Q(s,a),所以不需要环境模型,贪心策略为:
$$
\pi(s) = argmax_a q(s,a)
$$
前面提到过,MC方法通过平均样本的回报来解决强化学习的问题,体现在:
$$
Q(S_t,A_t) \leftarrow avg(Returns(S_t,A_t))
$$
通过试探性出发来评估生成动作状态价值Q(s,a)的代码如下,其中试探性出发体现在initial_state和initial_action的随机选取:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47# 试探性出发:
def monte_carlo_es(episodes):
# 维度对应:(playerSum【12~21】, dealerCard【1~10】, usableAce【0,1】, action【hit、stand】)
state_action_values = np.zeros((10, 10, 2, 2))
# Q(S,A)需要用到计数取均值,用1初始化,避免➗0
state_action_pair_count = np.ones((10, 10, 2, 2))
# 策略改进,在当前价值函数上贪心的选取并返回一个action
# 由于有Q(s,a)所以不需要环境模型信息(没有环境的模型信息意味着无法直接遍历所有的状态空间)
# 贪心策略为:π(s)=argmax_a q(s,a)
def behavior_policy(usable_ace, player_sum, dealer_card):
usable_ace = int(usable_ace)
player_sum -= 12
dealer_card -= 1
# state:s 即(player_sum, dealer_card, usable_ace)
# action:a 即缺省量,缺省是为了遍历a(因为argmax_a)
# 取avg,即实现平均样本回报
values_ = state_action_values[player_sum, dealer_card, usable_ace, :] / \
state_action_pair_count[player_sum, dealer_card, usable_ace, :]
# 贪心策略:π(S_t)= argmax_a Q(S_t,a)
return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# 对每一幕循环
for episode in tqdm(range(episodes)):
# 试探性出发:使每个(动作initial_action,状态initial_state)都可以被选为起点
# 随机生成每一幕的初始状态【usable_ace_player, player_sum, dealer_card】
initial_state = [bool(np.random.choice([0, 1])),
np.random.choice(range(12, 22)),
np.random.choice(range(1, 11))]
# 随机从【hit、stand】取一个策略动作
initial_action = np.random.choice(ACTIONS)
# 只在第一轮(即episode==0时)用target_policy_player(Q均为0,没法贪心)
# 其余时刻使用贪心动作选取:behavior_policy
current_policy = behavior_policy if episode else target_policy_player
# 根据初始状态(initial_state,initial_action)和current_policy生成一幕序列trajectory
_, reward, trajectory = play(current_policy, initial_state, initial_action)
# 对幕中的每一步循环
for (usable_ace, player_sum, dealer_card), action in trajectory:
usable_ace = int(usable_ace)
player_sum -= 12
dealer_card -= 1
# update values of state-action pairs
state_action_values[player_sum, dealer_card, usable_ace, action] += reward
state_action_pair_count[player_sum, dealer_card, usable_ace, action] += 1
# Q(St,At)= avg(returns(St,At))
return state_action_values / state_action_pair_count
代码中有一个小trick,即1
2
3
4
5
6# -12和-1的操作是为了对齐数组下标
# 因为player_sum永远大于11,dealer_card永远大于1
# 因为state_action_values和state_action_pair_count的维度均为【10,10,2,2】
# 所以需要对齐
player_sum -= 12
dealer_card -= 1
On-Policy
为了使MC收敛,上面做了两个强假设,而事实上,试探性出发虽然能够起到explore的作用,但其随机选择的(S,A)容易不符合实际(这是显然的,尤其是在状态空间过大时,最优策略不可能分摊给每一个二元组一定的选择概率)。
为了避免很难被满足的试探性出发假设,唯一的一般性解决方法就是智能体能够持续不断的选择所有可能的动作。rf提出了On-Policy和Off-Policy两种方法来保证这一点,这里首先介绍On-Policy方法。
在On-Policy中,用于生成采样数据序列的策略和用于实际决策的待评估和改进策略相同,即action-policy=target-policy。
实现代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21# 直接使用target-policy生成episode序列,未涉及优化policy
def monte_carlo_on_policy(episodes):
states_usable_ace = np.zeros((10, 10))
states_usable_ace_count = np.ones((10, 10))
states_no_usable_ace = np.zeros((10, 10))
states_no_usable_ace_count = np.ones((10, 10))
for i in tqdm(range(0, episodes)):
# on-policy:生成player_trajectory和评估的策略同为:target_policy_player
_, reward, player_trajectory = play(target_policy_player)
for (usable_ace, player_sum, dealer_card), _ in player_trajectory:
player_sum -= 12
dealer_card -= 1
if usable_ace:
states_usable_ace_count[player_sum, dealer_card] += 1
states_usable_ace[player_sum, dealer_card] += reward
else:
states_no_usable_ace_count[player_sum, dealer_card] += 1
states_no_usable_ace[player_sum, dealer_card] += reward
return states_usable_ace / states_usable_ace_count, states_no_usable_ace / states_no_usable_ace_count
Off-Policy
与On-Policy不同,Off-Policy中用于评估或者改进的策略与生成采样数据的策略是不同的,即生成的数据“离开了(off)”待优化策略所决定的决策序列轨迹。
为了实现从行动策略b得到的多幕样本序列取预测目标策略π,这就要求:对任意的π(a|s)>0,均有b(a|s)>0,换句话说,通过行动策略b采样到的序列需要覆盖掉目标策略π下的样本空间。
虽然行动策略b能够做到采样并覆盖,但其采样规律与目标策略毕竟不同,这时候就需要引入一个调和参数$\rho_{t:T-1}$,其称为importance ratio,定义如下,即一幕(t~T-1)时刻中在两种策略下产生同样的(状态,动作)二元组的概率之比:
$$
\rho_{t:T-1} =\prod_{k=t}^{T-1} \frac{\pi(A_k|S_k)}{b(A_k|S_k)}
$$
有了重要度采样参数,为了取平均,预测(动作)状态价值又引申出了两种方法,区分为在取平均时,选幕长还是采样比之和作为基:
- 普通重要度采样 ordinary_sampling:无偏估计;方差无界
$$
V(s)=\frac{\sum_{t \in T(s)} \rho_{(t:T(t)-1)}G_t}{|T(s)|}
$$ - 加权重要度采样 weighted_sampling:有偏估计,偏差逐渐收敛到0;方差能收敛到0(更偏好该方法)
$$
V(s)=\frac{\sum_{t \in T(s)} \rho_{(t:T(t)-1)}G_t}{\sum_{t \in T(s)} \rho_{(t:T(t)-1)}}
$$
回到游戏背景中,行动策略b与目标策略分别实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14# 玩家目标策略:通过玩家此时的手牌和player_sum决定策略(要牌/停牌)
# 用于off-policy的目标策略π
def target_policy_player(usable_ace_player, player_sum, dealer_card):
return POLICY_PLAYER[player_sum]
# 玩家行动策略:用于生成幕序列探索
# 用于off-policy的行为策略b
# 保证了ε软性,即每个action都有被选取到的概率
def behavior_policy_player(usable_ace_player, player_sum, dealer_card):
# 二项分布(1,0.5)执行一次p=0.5的实验
# 随机返回0/1
if np.random.binomial(1, 0.5) == 1:
return ACTION_STAND
return ACTION_HIT
评估对比代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57# Monte Carlo Sample with Off-Policy
def monte_carlo_off_policy(episodes):
# 给定初始状态【ace,player_sum,dealer_card】
initial_state = [True, 13, 2]
# 记录采样比、回报列表
rhos = []
returns = []
# 对每一幕循环
for i in range(0, episodes):
# 根据行动策略b:behavior_policy_player生成一幕数据:player_trajectory
_, reward, player_trajectory = play(behavior_policy_player, initial_state=initial_state)
# get the importance ratio
# 重要度采样
numerator = 1.0 # 分子为策略π
denominator = 1.0 # 分母为策略b
# 对幕中的每一步循环,累乘重要度采样
for (usable_ace, player_sum, dealer_card), action in player_trajectory:
if action == target_policy_player(usable_ace, player_sum, dealer_card):
# 行为策略b为(1,0.5)的二项分布,连乘的概率量为0.5
denominator *= 0.5
else:
# 由于π(action | state)即target_policy在本例中是确定的
# 即对一个state输入,其在两个action的概率采样中必然一个为1一个为0
# 所以一旦b产生的行为action不等于π的action
# 即证明此时π(A_k|S_k)==0
# 由于重要度采样比中使用连乘,所以π对应的分子直接为0
numerator = 0.0
break
# 重要度采样比
rho = numerator / denominator
# 重要度采样比序列
rhos.append(rho)
# 回报序列
returns.append(reward)
rhos = np.asarray(rhos)
returns = np.asarray(returns)
# 加权回报
weighted_returns = rhos * returns
# 对weighted_returns进行累加
# accumulate(【1,2,3】)=【1,3,6】
weighted_returns = np.add.accumulate(weighted_returns)
rhos = np.add.accumulate(rhos)
# 普通重要性采样
ordinary_sampling = weighted_returns / np.arange(1, episodes + 1)
# 加权重要性采样
# errstate(**kwargs) 用于浮点错误处理的上下文管理器
with np.errstate(divide='ignore',invalid='ignore'):
weighted_sampling = np.where(rhos != 0, weighted_returns / rhos, 0)
return ordinary_sampling, weighted_sampling
实验结果
最优策略如书中所示,这里仅展示off-policy下的两种方法结果对比: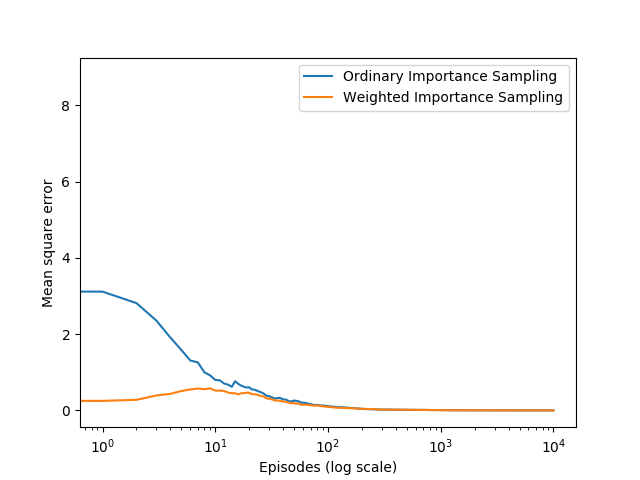
虽然两种方法误差最终均能收敛接近于0,但加权重要度采样在episode开始时也能保证一个较低的误差,是实践中常常选取的方法。
参考文献
[1] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

