强化学习：DP优化之价值迭代

Posted on | In | 215次阅读
Words count in article: 1.2k 字 | Reading time ≈ 4 min

上一篇博客以杰克租车问题为背景建模了策略迭代算法，策略迭代算法是一类以DP优化为基础并且能够收敛到最优策略$\pi_*$的算法，但是其存在着一些缺点。
比如：每一次迭代都涉及到了策略评估过程，从而导致需要多次遍历状态集合。
在租车问题中，只有两个租车场的情况下，遍历状态空间需要$O(n^4)$的复杂度（租车2*还车2=4），假如再扩大停车场数，算法复杂度将以幂指数级别递增！

价值迭代

事实上，在策略迭代算法中，我们无需等到算法完全收敛。在一般情况下，策略评估算法在执行够一定轮数之后对其DP策略将不会再产生任何影响。
所以核心问题变成了，如何在适当的时间节点提前阻断价值评估。

价值迭代算法应运而生。
价值迭代算法为：在一次遍历后即刻停止策略评估（对每个状态进行一次更新）
更新过程为：
$$
v_{k+1}(s) = max_a E[R_{t+1}+\gamma v_k(S_{t+1})| S_t=s,A_t=a]\\
\;= max_a\sum_{s’,r}p(s’,r|s,a)[r+\gamma v_k(s’)]
$$

算法流程为：

repeat：
∆ ← 0
对每一个 s ∈ S repeat:

v ← V(s)
$V(s) \leftarrow max_a\sum_{s’,r}p(s’,r|s,a)[r+\gamma V(s’)]$
∆ ← max(∆,|v-V(s)|)

until ∆<$\theta$
输出 $\pi = argmax_a\sum_{s’,r}p(s’,r|s,a)[r+\gamma V(s’)]$

从算法中可以看到，其与策略评估不同之处在于：算法仅执行一遍价值评估，通过遍历行为空间，选取最大的状态价值赋值。

下面我们从实际的赌徒问题中评估价值迭代算法。

赌徒问题

问题背景

赌徒连续抛硬币，正面朝上获得赌资，反面朝上失去赌资，直到赢到100或输完。
该问题可以视为一个无折扣的有限MDP问题：

状态空间：赌徒的赌资：{1、2、3…99}
行为：下注金额：{1、2、3…min{s,100-s}} (下注金额最多不会超过距离获胜的差距)
收益：赢到100：+1，其余：0
状态价值：状态s下获胜的概率。
策略：当前持有赌资的下注金额。

超参数

根据问题背景，超参数设定如下：

1
2
3
4
5
6
7
8
# 赢钱目标
GOAL = 100

# 这里包括了0和100，仅仅是为了方便作图
STATES = np.arange(GOAL + 1)

# 硬币正面朝上的概率
HEAD_PROB = 0.4

价值更新

第一部分对算法的描述中说到：价值迭代算法只对状态进行一次价值更新，随即阻断。
在该问题中，参考价值迭代算法，价值更新的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# state value即状态价值：记录状态s下获胜的概率。
state_value = np.zeros(GOAL + 1)
# goal状态下的获胜概率必然为1.0
state_value[GOAL] = 1.0
sweeps_history = []

while True:
    old_state_value = state_value.copy()
    sweeps_history.append(old_state_value)
    # 对每一个 s ∈ S循环：
    for state in STATES[1:GOAL]:
        # 当前状态的行为空间上界不会超过：持有赌资/距离获胜所需金额
        actions = np.arange(min(state, GOAL - state) + 1)
        # 遍历行为空间，目的是找出max_a
        action_returns = []
        for action in actions:
            # p:HEAD_PROB、(1 - HEAD_PROB)
            # r：0
            # V'(s)：后继状态价值state_value[state +(赢)\-（输） action]
            action_returns.append(
                HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])
        # 找出所有行为a下的max—value
        new_value = np.max(action_returns)
        state_value[state] = new_value
    delta = abs(state_value - old_state_value).max()
    # 价值收敛
    if delta < 1e-9:
        sweeps_history.append(state_value)
        break

与策略迭代中的价值评估做一个对比：

  • 策略迭代中，价值评估仅关注在当前状态S下执行一个确定动作后产生的状态S’，进而遍历S’产生状态价值之和决定V(S)。
  • 价值迭代中，价值评估关注在当前状态S下，执行全部动作空间后产生的状态价值列表L(S’)，进而取L(S’)中的最大值来决定V(S)。

从而使价值迭代实现了一次执行，直接阻断的效益。

计算策略

赌徒背景下的策略为赌资到下注金额的映射。

最优策略$\pi = argmax_a\sum_{s’,r}p(s’,r|s,a)[r+\gamma V(s’)]$
仔细观察，其与上面的价值迭代过程$V(s) \leftarrow max_a\sum_{s’,r}p(s’,r|s,a)[r+\gamma V(s’)]$的唯一不同在于$argmax_a$，所以代码结构相同，最后取下标即可。

实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
# compute the optimal policy
policy = np.zeros(GOAL + 1)
for state in STATES[1:GOAL]:
    actions = np.arange(min(state, GOAL - state) + 1)
    action_returns = []
    for action in actions:
        action_returns.append(
            HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])
    # action_returns从1开始（0代表输光），np.round保留5位小数
    # 取action_returns最大值的下标
    policy[state] = actions[np.argmax(np.round(action_returns[1:], 5)) + 1]

结果

结果如图所示：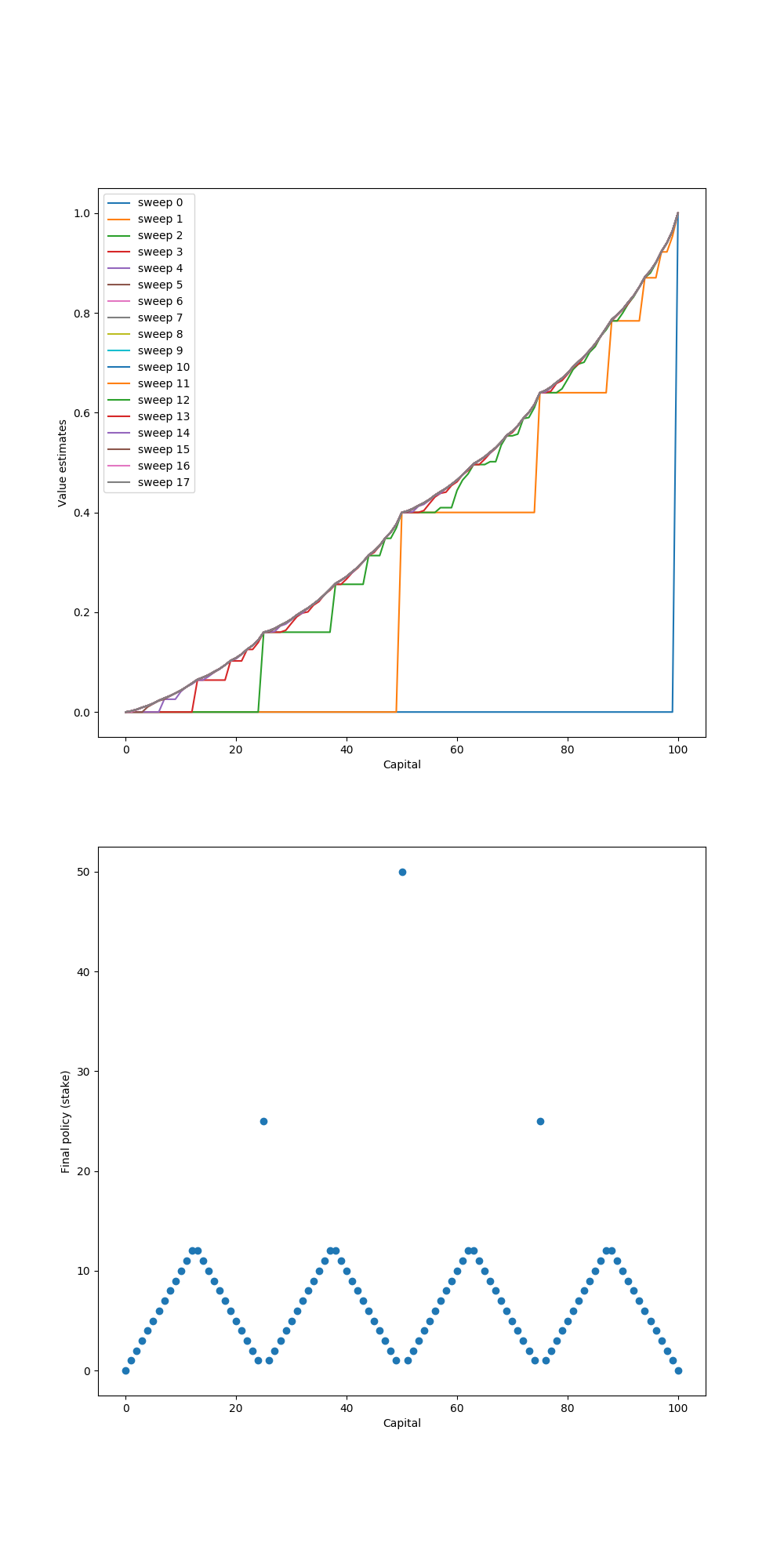
Alt text

参考文献

[1] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

小手一抖⬇️