这片博客我们以例4.2的杰克租车问题为例来讲述策略迭代算法。
策略迭代
策略迭代=评估+改进。
在DP的背景下,策略迭代算法的描述如下:
初始化
初始化状态价值以及策略(行为)
对$s \in S$,任意初始化$V(s) \in R、π(s) \in A(s)$
策略评估
所谓策略评估,即:在现有的策略$\pi$下,估计每个状态的状态价值$V(s)$
评估算法:
循环:对每个状态s使用如下方法进行评估:
$$
V(s) \leftarrow \sum_{s’,r}p(s’,r|s,π(s))[r+γV(s’)]
$$
评估收敛的依据如下,其中$\theta$为决定估计精度的收敛基准数
$$
|V(s)_{old}-V(s)|<\theta
$$
策略改进
所谓策略改进,即:通过现有的状态价值$V(s)$,改进策略行为$\pi(s)$
改进算法:
policyStable $\leftarrow$ true #判断策略是否稳定(收敛)
循环:对每个状态s使用如下方法进行评估:即在状态s下选出能使累计收益最大的动作a作为新的策略
$$
\pi(s) \leftarrow argmax_a \sum_{s’,r}p(s’,r|s,π(s))[r+γV(s’)]\\
if \; \pi_{old} \neq \pi(s): policyStable \leftarrow false
$$
评估收敛的依据如下:
$$
if \; policyStable = true :返回\pi \approx \pi_*
$$
若未收敛,则重新返回策略评估。
至此,基于DP的策略迭代算法的主要框架皆已讲述完毕,下面我们将其应用到实际问题中。
问题背景
问题背景为an introduction一书的例4.2,杰克租车问题。
梗概:杰克有两个租车场:
状态空间:两个场持有的车的数量
动作:将一部分车从A(或B)场移动到B(或A)场
收益:每租出一辆车+10,每移动一辆车-2
其中每个场的租车/还车请求符合泊松分布
问题建模
超参数
原始问题带有很多限制,所以首先进行超参数设定。
使用到的超参数如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30# 每个场的车容量
MAX_CARS = 20
# 每晚最多移动的车数
MAX_MOVE_OF_CARS = 5
# A场租车请求的平均值
RENTAL_REQUEST_FIRST_LOC = 3
# B场租车请求的平均值
RENTAL_REQUEST_SECOND_LOC = 4
# A场还车请求的平均值
RETURNS_FIRST_LOC = 3
# B场还车请求的平均值
RETURNS_SECOND_LOC = 2
# 收益折扣
DISCOUNT = 0.9
# 租车收益
RENTAL_CREDIT = 10
# 移车支出
MOVE_CAR_COST = 2
# (移动车辆)动作空间:【-5,5】
actions = np.arange(-MAX_MOVE_OF_CARS, MAX_MOVE_OF_CARS + 1)
# 租车还车的数量满足一个poisson分布,限制由泊松分布产生的请求数大于POISSON_UPPER_BOUND时其概率压缩至0
POISSON_UPPER_BOUND = 11
# 存储每个(n,lamda)对应的泊松概率
poisson_cache = dict()
泊松分布
泊松分布的概率式为:
$$
P(X = n) = \frac{\lambda^n}{n!}e^{-\lambda}
$$
其可由scipy.stats库中的poisson模块产生,为了避免重复调用,我们使用一个字典来记录每个状态下的概率值:1
2
3
4
5
6
7def poisson_probability(n, lam):
global poisson_cache
key = n * 10 + lam
if key not in poisson_cache:
# 计算泊松概率
poisson_cache[key] = poisson.pmf(n, lam)
return poisson_cache[key]
计算状态价值
计算状态价值的函数代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67def expected_return(state, action, state_value, constant_returned_cars):
"""
@state: 状态定义为每个地点的车辆数
@action: 车辆的移动数量【-5,5】,负:2->1,正:1->2
@stateValue: 状态价值矩阵
@constant_returned_cars: 将还车的数目设定为泊松均值,替换泊松概率分布
"""
# initailize total return
returns = 0.0
# 移动车辆产生负收益
returns -= MOVE_CAR_COST * abs(action)
# 移动后的车辆总数不能超过20
NUM_OF_CARS_FIRST_LOC = min(state[0] - action, MAX_CARS)
NUM_OF_CARS_SECOND_LOC = min(state[1] + action, MAX_CARS)
# 遍历两地全部的可能概率下(<11)租车请求数目
for rental_request_first_loc in range(POISSON_UPPER_BOUND):
for rental_request_second_loc in range(POISSON_UPPER_BOUND):
# prob为两地租车请求的联合概率
# 即:1地请求租车rental_request_first_loc量且2地请求租车rental_request_second_loc量
prob = poisson_probability(rental_request_first_loc, RENTAL_REQUEST_FIRST_LOC) * \
poisson_probability(rental_request_second_loc, RENTAL_REQUEST_SECOND_LOC)
# 两地原本的车的数量
num_of_cars_first_loc = NUM_OF_CARS_FIRST_LOC
num_of_cars_second_loc = NUM_OF_CARS_SECOND_LOC
# 有效的租车数目必须小于等于该地原有的车辆数目
valid_rental_first_loc = min(num_of_cars_first_loc, rental_request_first_loc)
valid_rental_second_loc = min(num_of_cars_second_loc, rental_request_second_loc)
# 计算回报,更新两地车辆数目变动
reward = (valid_rental_first_loc + valid_rental_second_loc) * RENTAL_CREDIT
num_of_cars_first_loc -= valid_rental_first_loc
num_of_cars_second_loc -= valid_rental_second_loc
# 如果还车数目为泊松分布的均值
if constant_returned_cars:
# 两地的还车数目均为泊松分布均值
returned_cars_first_loc = RETURNS_FIRST_LOC
returned_cars_second_loc = RETURNS_SECOND_LOC
# 还车后总数不能超过车场容量
num_of_cars_first_loc = min(num_of_cars_first_loc + returned_cars_first_loc, MAX_CARS)
num_of_cars_second_loc = min(num_of_cars_second_loc + returned_cars_second_loc, MAX_CARS)
# 核心:
# 策略评估:V(s) = p(s',r|s,π(s))[r + γV(s')]
returns += prob * (reward + DISCOUNT * state_value[num_of_cars_first_loc, num_of_cars_second_loc])
# 否则计算所有泊松概率分布下的还车空间
else:
for returned_cars_first_loc in range(POISSON_UPPER_BOUND):
for returned_cars_second_loc in range(POISSON_UPPER_BOUND):
prob_return = poisson_probability(
returned_cars_first_loc, RETURNS_FIRST_LOC) * poisson_probability(returned_cars_second_loc, RETURNS_SECOND_LOC)
num_of_cars_first_loc_ = min(num_of_cars_first_loc + returned_cars_first_loc, MAX_CARS)
num_of_cars_second_loc_ = min(num_of_cars_second_loc + returned_cars_second_loc, MAX_CARS)
# 联合概率为【还车概率】*【租车概率】
prob_ = prob_return * prob
returns += prob_ * (reward + DISCOUNT *
state_value[num_of_cars_first_loc_, num_of_cars_second_loc_])
return returns
总而言之,由于状态空间的决定涉及到【租车】+【还车】两个行为,所以需要在遍历满足泊松分布租车请求的基础上继续遍历满足泊松分布的还车请求来实现对状态价值的评估,算法复杂度可达$O(n^4)$!
策略评估
在能计算出状态价值之后,进行策略评估便不是什么困难的事情,参考第一部分中的算法,策略评估的实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15# 策略评估(in-place)
# 未改进前,第一轮policy全为0,即【0,0,0...】
while True:
old_value = value.copy()
for i in range(MAX_CARS + 1):
for j in range(MAX_CARS + 1):
# 更新V(s)
new_state_value = expected_return([i, j], policy[i, j], value, constant_returned_cars)
# in-place
value[i, j] = new_state_value
# 比较V_old(s)、V(s)
max_value_change = abs(old_value - value).max()
# 收敛
if max_value_change < 1e-4:
break
策略改进
在上一部分可以看到,策略policy全都是0,如不进行策略改进,其必然不会收敛到实际最优策略。
改进部分的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22# 策略改进
policy_stable = True
# i、j分别为两地现有车辆总数
for i in range(MAX_CARS + 1):
for j in range(MAX_CARS + 1):
old_action = policy[i, j]
action_returns = []
# actions为全部的动作空间,即【-5、-4...4、5】
for action in actions:
if (0 <= action <= i) or (-j <= action <= 0):
action_returns.append(expected_return([i, j], action, value, constant_returned_cars))
else:
action_returns.append(-np.inf)
# 找出产生最大动作价值的动作
new_action = actions[np.argmax(action_returns)]
# 更新策略
policy[i, j] = new_action
if policy_stable and old_action != new_action:
policy_stable = False
# 策略收敛
if policy_stable:
break
结果
结果如图: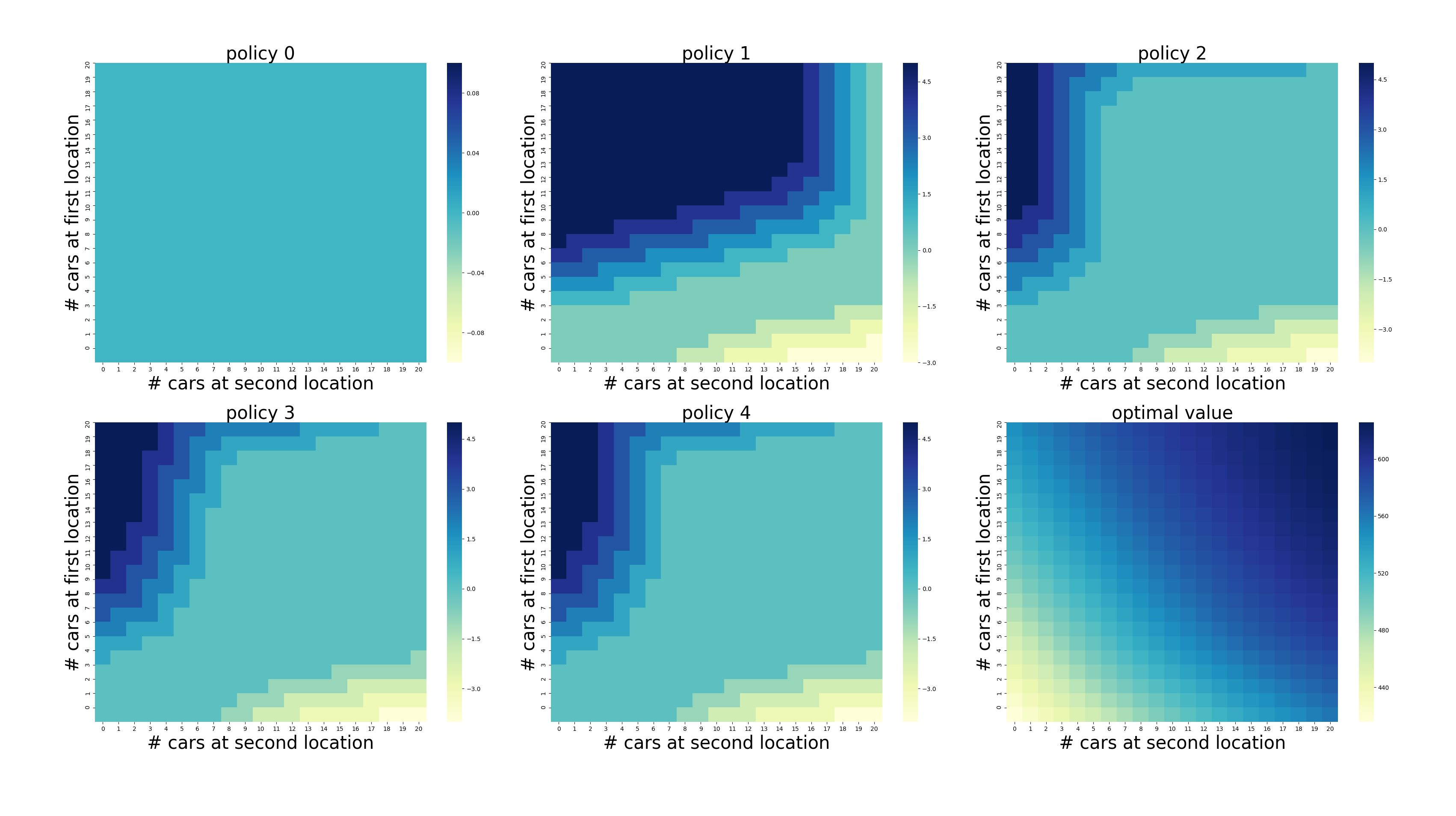
正数代表从1场移动到2场,负数代表从1场移动到2场。
代码在运行完5轮后达到收敛,即policy4可视为收敛策略。
由于1场的租车和还车请求均为3,而2场的租车请求为4、还车请求为2,所以更偏向于从1场向2场移动车。
参考文献
[1] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

