这一节我们介绍k臂赌博机问题,首先来熟悉一下问题的背景知识
问题背景
重复的在k个选项或动作(k个老虎机的杆)中进行选择,每次做出选择之后都会得到一定数额的收益,我们的目的是在一段时间内最大化总收益的期望。
bandit建模
在用代码实现赌博机时,我们需要考虑多方因素,下面先列出一个bandit初始化时需要考虑到的各种参数:1
2
3
4
5
6
7
8
9
10
11
12
13
14def __init__(self, k_arm=10, epsilon=0., initial=0., step_size=0.1, sample_averages=False, UCB_param=None,
gradient=False, gradient_baseline=False, true_reward=0.):
self.k = k_arm
self.step_size = step_size
self.sample_averages = sample_averages
self.indices = np.arange(self.k)
self.time = 0
self.UCB_param = UCB_param
self.gradient = gradient
self.gradient_baseline = gradient_baseline
self.average_reward = 0
self.true_reward = true_reward
self.epsilon = epsilon
self.initial = initial
- k_arm:赌博机的臂数,其决定了可选动作空间的大小,例如当k_arm=10时意味着:每个时刻有10个可选动作,其分别决定着不同的收益。
- epsilon:在每次进行动作选取时,一个朴素的思想就是每次都选带来最大收益的动作,即$A_t = agrmax_aQ_t(a)$,我们称之为“贪心”,贪心有利于exploit但不利于explore,为了平衡开发和试探,可采用ε-greedy方法进行动作的选择,即在每个时刻,使用1-ε的概率选取最优动作,使用ε的概率选取随机动作。
- initial:在对动作价值估计之前,我们通常为每个动作的价值Q(a)初始化为0。使用乐观初始值(即高于真实价值的均值)估计会去鼓励bandit进行explore,因为无论哪种动作被选取,其带来的收益均要小于乐观初始值,因此bandit会转而采取另一种动作,从而使每一个动作在收敛之前都被尝试很多次。
- step_size:步长参数,有固定步长和非固定步长两种类别可选。用于动作估计值的更新:$Q_{n+1} = Q_n + stepsize*(R_n - Q_n)$
- sample_averages:用非固定步长$1/n$作为步长参数$stepsize$,用于动作估计值的更新:$Q_{n+1} = Q_n + (R_n - Q_n)/n$
- UCB_param:UCB即对应置信度上界,即动作的选取从$A_t = agrmax_aQ_t(a)$改变为$A_t = agrmax_a[Q_t(a)+c\sqrt{lnt/N_t(a)}]$,其中UCB_param即动作选取公式中的c,可解释为:平方根项是对a动作值估计的不确定性或方差的度量,参数c决定了置信水平,但随着a选取次数$N_t(a)$的增多,其不确定性会逐渐减少。
- gradient:对应梯度赌博机算法,算法中每个动作被选取的概率为softmax分布所确定:$P(A_t=a) = e^{H_t(a)}/\sum_{b=1}^{k}e^{H_t(b)} = π_t(a)$,其中$π_t(a)$代表时刻t动作a被选择的概率,而$H_t(a)$则代表动作a的偏好函数。
- gradient_baseline:在梯度赌博机算法中,待学习的变量为偏好函数$H_t(a)$,可以把其理解为动作a的收益,但其本身不重要,重要的是一个动作对另一个动作的相对偏好。偏好函数的更新如下:$$
H_{t+1}(a) = H_t(a) + stepsize*(R_t - baseline)(1-π_t(A_t))
$$
当使用baseline时,baseline被赋值为到t为止的平均收益;不使用时则等于0。使用基准项可以实现缩减方差的作用,使算法快速收敛。
动作选取
对于一个MDP问题而言,其过程必定可以被建模为:
$$
S_t + A_t \rightarrow S_{t+1} + R_{t+1}
$$
所以首先来考虑动作的选取。
由bandit的模型基础可知,动作的选取由ε-greedy、UCB_param、gradient决定,我们可以直接给出如下的动作选取代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23# get an action for this bandit
def act(self):
if np.random.rand() < self.epsilon:
return np.random.choice(self.indices) # epsilon概率随机选取一个动作下标
# 基于置信度上界的动作选取
# At = agrmax_a [Qt(a)+c√(lnt/Nt(a))]
if self.UCB_param is not None:
UCB_estimation = self.q_estimation + \
self.UCB_param * np.sqrt(np.log(self.time + 1) / (self.action_count + 1e-5))
q_best = np.max(UCB_estimation) # 取UCB估值序列的最大值
return np.random.choice(np.where(UCB_estimation == q_best)[0]) #在相同的最大值中随机选取
# 梯度赌博机算法
# P{At=a} = e^Ht(a) / ∑_b e^Ht(b) = πt(a)
if self.gradient:
exp_est = np.exp(self.q_estimation)
self.action_prob = exp_est / np.sum(exp_est)
return np.random.choice(self.indices, p=self.action_prob) # 以概率表action_prob的概率在下标列表indices中选取
# 否则就直接选去估计值最大的动作
q_best = np.max(self.q_estimation)
return np.random.choice(np.where(self.q_estimation == q_best)[0])
价值更新
由bandit建模部分可以得知,在选取完动作后,与动作价值更新有关的参数为sample_averages、gradient、gradient_baseline,给出代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29# take an action, update estimation for this action
def step(self, action):
# generate the reward under N(real reward, 1)
reward = np.random.randn() + self.q_true[action]
self.time += 1
self.action_count[action] += 1
self.average_reward += (reward - self.average_reward) / self.time
if self.sample_averages:
# update estimation using sample averages
# 增量式实现(非固定步长1/n)
# Qn+1 = Qn + [Rn-Qn]/n
self.q_estimation[action] += (reward - self.q_estimation[action]) / self.action_count[action]
elif self.gradient:
one_hot = np.zeros(self.k)
one_hot[action] = 1
if self.gradient_baseline:
baseline = self.average_reward
else:
baseline = 0
# 梯度式偏好函数更新:
# 对action At:Ht+1(At) = Ht(At) + å(Rt-R_avg)(1-π(At))
self.q_estimation += self.step_size * (reward - baseline) * (one_hot - self.action_prob)
else:
# update estimation with constant step size
# 如过上面两种方法都没有选取,就选用常数步长更新
# Qn+1 = Qn + å(Rn-Qn)
self.q_estimation[action] += self.step_size * (reward - self.q_estimation[action])
return reward
对比评估
评估结果与an introduction书中所示类似,这里只给出一些结果:
测试四种方法的结果对比,可以看到,最优的结果出现在使用小步长+baseline时的情况。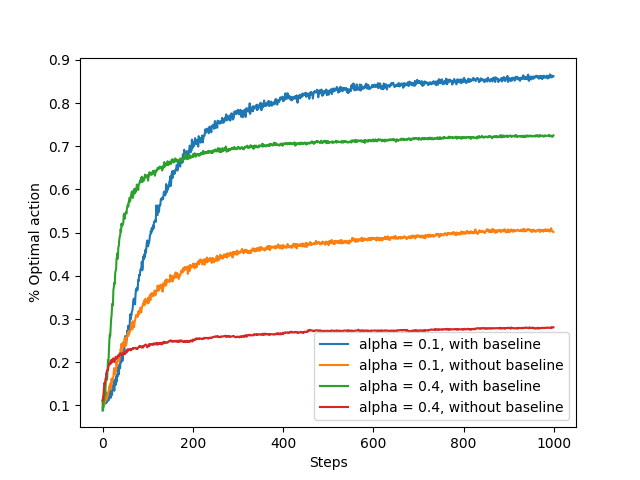
参考文献
[1]https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

