在有限马尔科夫决策这一部分,我们通过一个网格问题来理解分幕式问题的建模和求解过程。
网格问题
示例给出的长方形网格代表一个简单的有限MDP:
状态:网格中的格子代表一个状态
动作:在每个格子中都有{东、南、西、北}四个可选动作
收益:当agent执行动作后脱离了网格,其收益-1;当处在状态A或B时,执行任何动作都会转移至状态A’或B’,其收益分别为+10、+5;其余所有状态收益+0。
表格中‘φ’为空白
| A | B | φ | ||
|---|---|---|---|---|
| φ | ||||
| B’ | φ | |||
| φ | ||||
| A’ | φ |
我们的目的是计算出在每个网格中的状态价值,限定折扣系数:γ=0.9
超参数设计
在编写agent行为之前需要先设置一些全局变量,此处的全局变量共包括如下:
1 | # A、B、A‘、B’位置坐标 |
状态转换
网格问题的状态转换,即下述MDP:
$$
S_t + A_t → S_{t+1}, R_{t+1}
$$
我们用代码来实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14def step(state, action):
if state == A_POS: # A点会无条件转移到A',并且收益+10
return A_PRIME_POS, 10
if state == B_POS: # B点会无条件转移到B',并且收益+5
return B_PRIME_POS, 5
next_state = (np.array(state) + action).tolist()
x, y = next_state
if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:
reward = -1.0 # 出界收益-1
next_state = state # 出界状态不变
else:
reward = 0 # 其余收益+0
return next_state, reward
等概率下的状态价值
为了求解每个状态的状态价值,我们假定每个状态下选取东、南、西、北四个动作的概率相等,均为0.25。
邻接时刻的回报可以用递归的方式来表示:
$$
G_t = R_{t+1} + γR_{t+2} + γ^2R_{t+3} + …
= R_{t+1} + γG_{t+1}
$$
其在代码中通过new_value[i, j] += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])来实现
我们用代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23value = np.zeros((WORLD_SIZE, WORLD_SIZE))
# 训练至收敛
while True:
# keep iteration until convergence
new_value = np.zeros_like(value)
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
# 在每一格都执行东南西北走位,遍历该状态下的动作空间
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
# bellman equation
# 价值更新: Gt = Rt+1 + γGt+1
# t:即(i,j)所在位置,t+1:即(next_i, next_j)所在位置
# ACTION_PROB=0.25,即四个方向对价值更新的贡献相同
new_value[i, j] += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
# 收敛:sum新价值-sum旧价值变化 < 1e-4
if np.sum(np.abs(value - new_value)) < 1e-4:
draw_image(np.round(new_value, decimals=2))
plt.savefig('../images/figure_3_2.png')
plt.close()
break
# value记录上一轮价值
value = new_value
执行结果如下,可以看到,如果在网格中的每个状态中执行等概率的动作选取,其状态价值如下: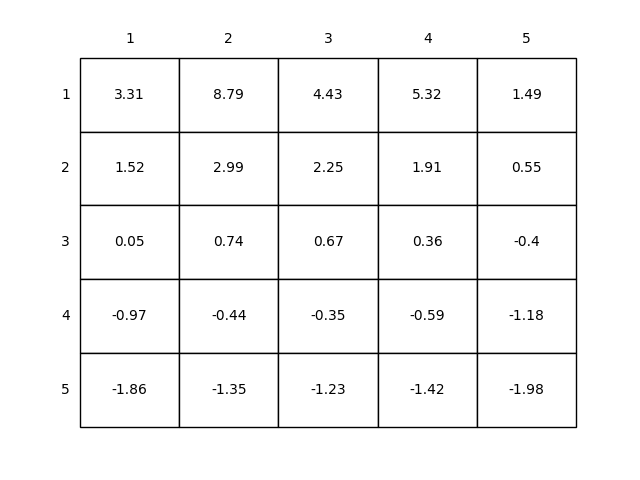
最优动作下的状态价值
上面展示了,在每个状态下动等概率选取动作的状态价值结果。
下面我们假定在每个状态下执行最优动作$A^*$,重新计算每个状态下的状态价值。
同样,邻接时刻的回报可以用递归的方式来表示:
$$
G_t = R_{t+1} + γR_{t+2} + γ^2R_{t+3} + …
= R_{t+1} + γG_{t+1}
$$
但这里我们选取最优价值$q^*$所对应的动作$A^*$,替换掉0.25的等概率动作选取。
代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18while True:
# keep iteration until convergence
new_value = np.zeros_like(value)
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
values = []
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
# value iteration
values.append(reward + DISCOUNT * value[next_i, next_j])
# 不使用等概率的(东南西北)动作选择,直接使用最优的动作
new_value[i, j] = np.max(values)
if np.sum(np.abs(new_value - value)) < 1e-4:
draw_image(np.round(new_value, decimals=2))
plt.savefig('../images/figure_3_5.png')
plt.close()
break
value = new_value
与上一节不同的是:在遍历动作空间ACTION时,变量values负责记录每个动作所产生的回报,而只有最大回报np.max(values)对应的最优动作会对价值更新产生贡献,即new_value[i, j] = np.max(values)。
执行结果如下,可以看到,如果在网格中的每个状态中执行最优的动作选取,其状态价值如下,相比等概率选取,执行最优极大的提高了每个状态下的状态价值: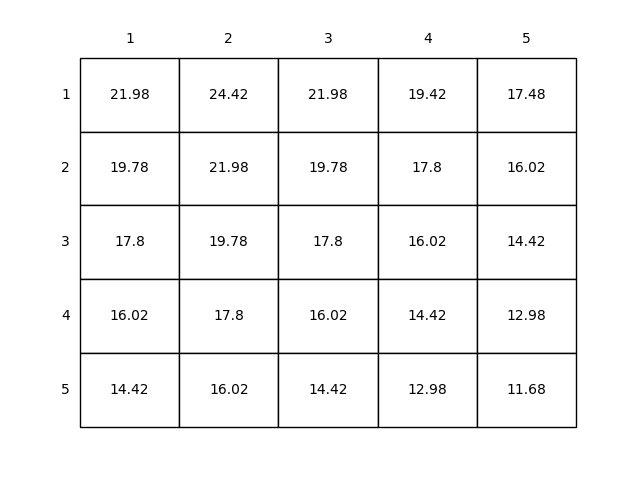
参考文献
[1] https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

