编译原理——基于SLR1的语法制导翻译及中间代码生成

Posted on | In | 次阅读
Words count in article: 6.1k 字 | Reading time ≈ 30 min

目标任务

实验项目

完成以下描述赋值语句SLR(1)文法语法制导生成中间代码四元式的过程。

1
2
3
4
5
G[A]:   A→V=E 
        E→E+T∣E-T∣T
        T→T*F∣T/F∣F 
        F→(E)∣i           
        V→i

设计说明

终结符号i为用户定义的简单变量，即标识符的定义。

设计要求

（1）构造文法的SLR(1)分析表，设计语法制导翻译过程，给出每一产生式对应的语义动作；
（2）设计中间代码四元式的结构；
（3）输入串应是词法分析的输出二元式序列，即某赋值语句“专题1”的输出结果，输出为赋值语句的四元式序列中间文件；
（4）设计两个测试用例（尽可能完备），并给出程序执行结果四元式序列。

实验过程

数据结构

在明确好编程思想后，首先需要确定下来的就是如何组织类及类成员，如何存储数据。
下面给出算符优先语法分析类class SLR的成员变量/函数及其设计说明：

类成员变量

成员变量 类型 备注
start str 文法开始符号
Vt set() 终结符号集合
Vn set() 非终结符号集合
V set() 文法全部符号集合，用于构造SLR分析表
rule dict{str: list[str]} 文法产生式规则
point str 即符号‘.’，用于构造项目集
first set() 文法的first集，用于构造follow集
follow set() 文法的follow集，用于解决冲突项目
C dict{int: dict{str:list[str]}} 记录有效项目集规范族
r dict{int: dict{str:str}}} 记录产生式序号，辅助生成action表中的r项
action dict{(int,str):str} 记录SLR分析表中的action动作，包括‘S’和‘r’
goto dict{(int,str):int} 记录SLR分析表中的goto动作，即记录待跳转的下一个项目集序号

类成员函数

成员函数 备注
init(self, start, Vn, Vt, rule) 类的构造函数，通过输入文法的开始符号、非终结符/终结符号集、产生式规则从而构造并返回SLR类
get_first(self) 构造first集合
get_follow(self) 构造follow集合
op_start(self) 构造有效项目集的第一步动作，即加入：‘.’+开始符号产生式
op_closure(self,c_j) 求c_j项目集的闭包
op_go(self,i,x) 实现Go(Ci ,x)函数功能
judge(self,i) 判断C[i]是否为终态，辅助构造有效项目集C
get_C(self) 生成有效项目集规范族C
get_r(self) 生成带序号的产生式，用于生成action表中的r部分
get_action(self) 构造分析表的action部分
get_goto(self) 构造分析表的goto部分
compile(self, symbol, word, log) 对输入语句进行语法分析，其中 symbol: 符号语句；word: 真实语句；log: 是否打印四元式

本次实验的重点在于下面几个成员函数的实现：

求c_j项目集的闭包
get_C(self): 自动生成有效项目集规范族C
get_action(self): 构造分析表的action部分
get_goto(self): 构造分析表的goto部分
compile(self, symbol, word, log): 对输入语句进行语法分析

求C[j]项目集的闭包

求C[j]项目集闭包，即实现closure(Cj)的功能，其算法如下：

$$
① C_i 的任何项目均属于closure(C_i)
$$

$$
② （重复）若A → α·X β(X∈V_n) ∈ closure(C_i) ,则X → ·λ ∈ closure(C_i)
$$

$$
③ C_i = closure(C_i)
$$

代码实现如下，上面三步在代码中有详细注释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def op_closure(self,c_j):
    #① C_i 的任何项目均属于closure(C_i)
    closure_i = c_j
    #② （重复）若A → α·X β(X∈V_n) ∈ closure(C_i) ,则X → ·λ ∈ closure(C_i)
    while(True):
        closure_i1=closure_i.copy()
        key_list = list(closure_i.keys())
        for A in key_list:
            for aXb in closure_i[A]:
                for j in range(len(aXb)-1):
                    if(aXb[j]==self.point and aXb[j+1] in self.Vn):
                        # 如何没有则新建一个key
                        if(aXb[j+1] not in closure_i.keys()):
                            closure_i.update({aXb[j + 1]:[]})
                            key_list.append(aXb[j + 1])
                        for l in rule[aXb[j+1]]:
                            temp = self.point+l
                            if(temp not in closure_i[aXb[j+1]]):
                                closure_i[aXb[j+1]].append(temp)
        # 重复,直至 closure(Ci)不再增大.
        if(closure_i != closure_i1):
            closure_i1 = closure_i.copy()
        else:
            # ③ C_i = closure(C_i)
            return closure_i

自动生成有效项目集规范族C

在SLR(1)分析过程中，前期准备中最重要的就是构建SLR(1)的有效项目集规范族C

根据生成算法，我们来对代码进行逐步实现

1.拓广文法,保证唯一初态.

1
2
3
4
# 拓广文法
self.rule['S'] = start + "#"
self.Vn.append('S')
self.start = 'S'

2.生成C0={S→ ·δ} ∪{S→ ·δ的闭包操作}

1
2
3
4
# 生成C0={S→ ·δ}
self.op_start()
# ∪ {S→ ·δ的闭包操作}
self.C[0]=self.op_closure(self.C[0])

3.重复以下过程,直至C不再增大为止.

Ci读操作,生成Cj1,Cj2,…….Cjn
Cj1,Cj2,…….Cjn闭包操作(若其中某项目集已经存在就略去)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
i = 0
j = 1
while(True):
    # 判断C[i]是否为终态
    if (i == j):
        break
    if(self.judge(i)==True):
        self.tC.append(i)
        i=i+1
        continue
    for v in self.V:
        c_j = self.op_go(i,v)
        if(len(c_j)!=0):
            closure_j = self.op_closure(c_j)
            flag = True
            if self.check_in_C(closure_j):
                flag=False
            if flag:
                self.C[j]=closure_j
                j = j + 1
            if (i<j):
                i=i+1
            else:
                break

到此，该文法下的有效项目集规范族已被完全构建，看一下预览：
Alt text
可以看到，拓广文法后产生的21个项目完全正确

构造分析表的action部分

SLR(1)文法的分析表包括action和Goto两个部分，这里先谈第一部分，即action部分的实现

action动作的添加主要分为三种情况：

1.若GO(Ci, a)=Cj a∈Vt, 置ACTION(i,a)=Sj

Sj:移进,把下一状态j和现输入符号a移入栈

2.若S→δ· ∈ Ck , (S为拓广文法开始符号) 置ACTION(k,#)=acc

acc:接受

3.若A→α·∈Ci , 且 a∈FOLLOW(A) , a∈Vt 置ACTION(i,a)=rj (A → α为第 j个产生式)

rj:归约,按第j产生式归约

所以我们的目的是，遍历文法Vt中的所有终结符号
在构造好的项目集C中找到对应情况下的（项目，符号）组合，为该组合添加对应动作

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 构造分析表的action部分
    def get_action(self):
        # 若GO(Ci, a)=Cj  a∈Vt, 置ACTION(i,a)=Sj
        for i in self.C.keys():
            for a in self.Vt:
                j = self.GO(i,a)
                if(j!=-1):
                    self.action[(i,a)]='S'+str(j)

        # 若A→α·∈Ci , 且 a∈FOLLOW(A)
        #  a∈Vt 置ACTION(i,a)=rj (A → α为第 j个产生式)
        for i in self.C:
            for A in self.C[i].keys():
                for item in self.C[i][A]:
                    # 项目最后一个为点 '·'
                    if(item[-1] == self.point):
                        for a in self.follow[A]:
                            # 找到对应的规约产生式
                            for j in self.r.keys():
                                temp = {A:item[:-1]}
                                if(self.r[j] == temp):
                                    self.action[(i,a)]='r'+str(j)


        # 若S→δ·∈ Ck ,(S为拓广文法开始符号）
        # 置ACTION(k,#)=acc
        omiga = rule[self.start]+self.point
        for k in self.C:
            for key in self.C[k].keys():
                if(key==self.start and omiga in self.C[k][key]):
                    self.action[(k,'#')]="acc"

构造分析表的Goto部分

Goto部分是在遍历文法Vn中的所有非终结符号时产生的动作，即状态S面临文法符号x时下一状态

Goto动作的添加仅对应一种情况：

若GO(Ci,A)=Cj , A∈Vn ,置GOTO(i,A)=j

代码实现如下：

1
2
3
4
5
6
7
8
# 构造分析表的goto部分
def get_goto(self):
    # 若GO(Ci, A)=Cj  A∈Vn, 置GOTO(i,A)=j
    for i in self.C.keys():
        for A in self.Vn:
            j = self.GO(i, A)
            if (j != -1):
                self.goto[(i, A)] = j

到此，我们已经构造好了SLR(1)分析表的所有部分，对于该题文法下的分析表，预览如下：
Alt text
Alt text

可对比上面生成的项目集，结果完全正确！

语法分析

在SLR类构建完毕之后，下面我们便可以通过接收输入来进行语法分析过程。

控制输入

根据题干要求，输入参数应为词法分析器所输出的二元组，所以这里对分析函数的参数列表构建如下，其中，word代表真实符号，symbol代表根据真实符号所转化的定义符号：

1
def compile(self, symbol, word, log)

举个例子，对于输入语句：X = A*(B+C)+D而言：

1
2
symbol : i=i*(i+i)+i
word : X=A*(B+C)+D

可以看出，symbol的作用在于进行语法分析，而word的作用在于生成四元式。

当然，这实现起来很简单，只需要在读如文件时控制读如组合即可，代码如下：

1
2
3
4
5
6
7
8
test_words = ""
test_symbol = ""
f = open("in2.0.txt",'r')
while(True):
    t = f.readline().strip('\n')
    if(t == ''): break
    test_symbol += t[0]
    test_words += t[-1]

对于如下格式的二元组输入：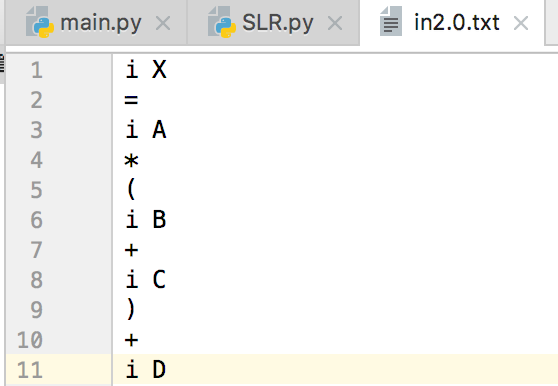
Alt text

可以看到这样的拼接结果：
Alt text

SLR(1)分析

SLR(1)的分析过程与LR(0)相同，需要两个栈来辅助分析，分别是：状态栈、符号栈
分析过程如图：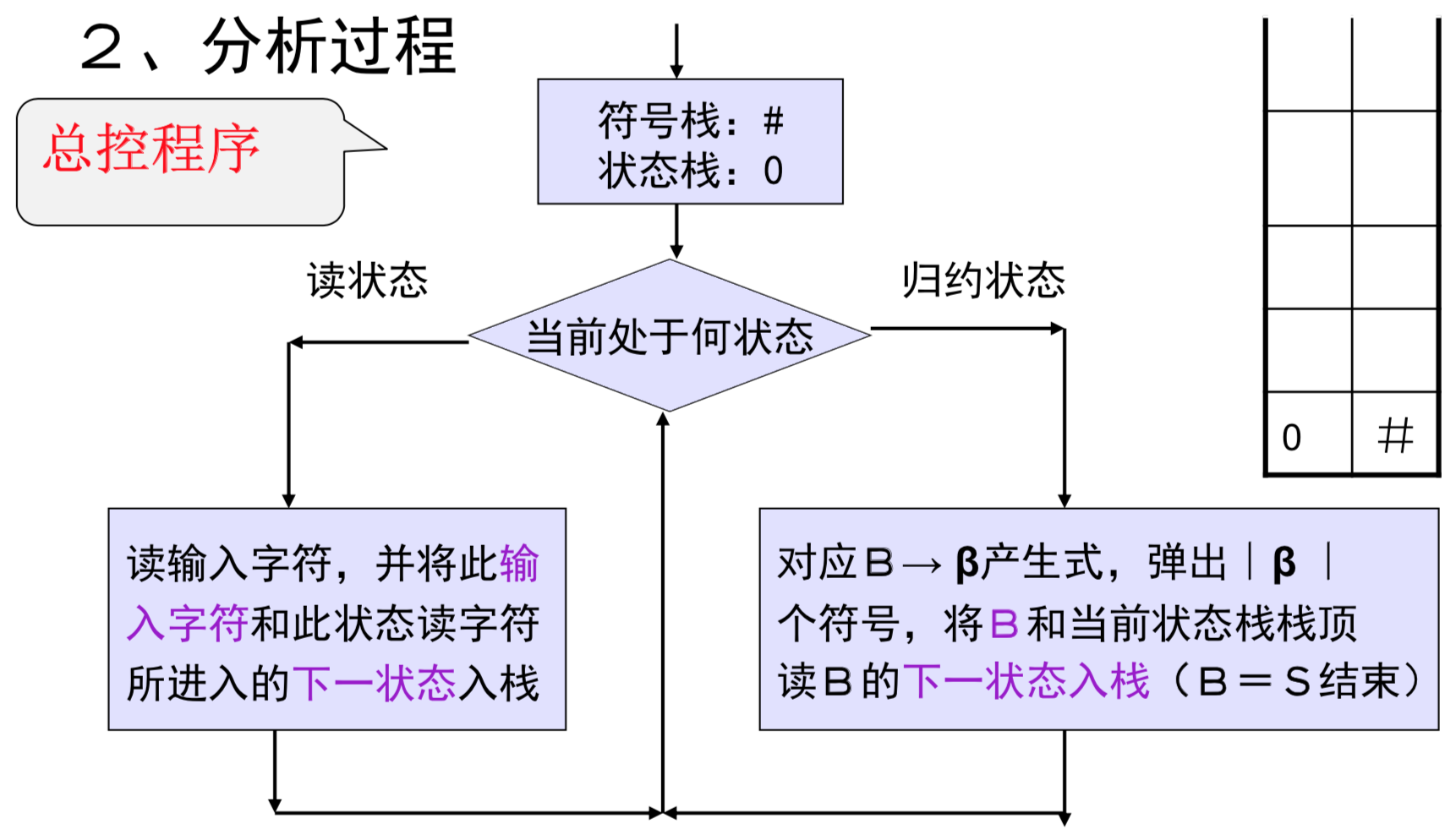
Alt text

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# SLR（1）法分析
# symbol: 符号语句 word: 真实语句
def compile(self, symbol, word, log):

    # 补充#
    symbol+="##"

    # 状态栈
    state = ['0']
    # 符号栈
    charater = ['#']

    #输入串下标
    k=0
    while(True):
        state_now = eval(state[len(state)-1])

        input_ch = symbol[k]

        if ((state_now,input_ch) in self.action.keys()):
            action = self.action[(state_now, input_ch)]
        else:
            action='-1'

        if(action[0]=='S'):
            #if(input_ch != '#'):
            k = k+1
            charater.append(input_ch)
            state.append(action[1:])
            continue

        elif(action[0]=='r'):
            # 规约动作r
            r = {}
            r = self.r[eval(action[1])]
            # 规约长度
            lenth = 0
            # 规约终结符
            substitude = ''
            r_rule=''
            for left in r.keys():
                substitude = left
                for right in r[left]:
                    r_rule+=right


            for i in range(len(r_rule)):
                charater.pop()
                state.pop()

            # 新规约终结符进符号栈
            charater.append(substitude)
            new_state = self.goto[(eval(state[len(state)-1]),substitude)]
            state.append(str(new_state))

        elif(action=='acc'):
            return True

        else:
            return False

其中，substitute和r_rule记录了每次规约时所选用的产生式substitute -> r_rule
所以根据此，我们可以去匹配生成对应的四元式组。

由课上所学可知，运算赋值语句文法每次规约时产生的对应动作如下：
Alt text
Alt text

用代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 根据规约规则r_rule决定执行动作, log为分析开关
   # 预定义.PLACE变量
   if log == True:
       E_place = []
       F_place = []
       V_place = []
       T_place = []
       t = 0 #temp计数器

   # 添加至上段中的while(True)中
   if log==True:
       # ② A →V=E
       if (substitude == 'A' and r_rule == "V=E"):
           print("( =, "+E_place.pop()+", ,"+V_place.pop()+" )")

       # ③ E(1)→E(2)+T
       elif (substitude == 'E' and r_rule == "E+T"):
           E1_place = "temp"+str(t)
           t=t+1
           print("( +, "+E_place.pop()+", "+T_place.pop()+", "+E1_place+" )")
           E_place.append(E1_place)

       # ④ E → T
       elif (substitude == 'E' and r_rule == "T"):
           E_place.append(T_place.pop())

       # ⑤ T(1)→ T(2)*F
       elif (substitude == 'T' and r_rule == "T*F"):
           T1_place = "temp"+str(t)
           t=t+1
           print("( *, "+T_place.pop()+", "+F_place.pop()+", "+T1_place+" )")
                       T_place.append(T1_place)

       # ⑥ T → F
       elif (substitude == 'T' and r_rule == "F"):
           T_place.append(F_place.pop())

       # ⑦ F →(E)
       elif (substitude == 'F' and r_rule == "(E)"):
            F_place.append(E_place.pop())

       # ⑧ F → i
       elif (substitude == 'F' and r_rule == "i"):
            F_place.append(word[k-1])

       # ⑨ V →i
       elif (substitude == 'V' and r_rule == "i"):
           V_place.append(word[k-1])

这里需要注意的一点是如何区分诸如E(1)→E(2)+T规则中的（1）和（2）
我的解决方法为：用栈结构来存储各个place变量。
根据运算赋值文法的特点，后产生的E一定会被先规约用掉，所以用栈来模拟可以保证先产生的E不被后续的E所覆盖。

到此，本次实验的SLR类已经被完全构建完毕。

SLR类分析

测试

我们以语句：X=A*(B+C)+D为例
对其进行词法分析，首先得到二元组结果文件如下：
Alt text

经过文件组织拼接后，调用函数

1
slr.compile(symbol=test_symbol,word=test_words,log=True)

得到输出结果如下：
Alt text

为了详细分析，通过适当调整输出来观测状态栈、符号栈的变化，结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/Library/Frameworks/Python.framework/Versions/3.6/bin/python3.6 /Users/jiahaonan/Desktop/大三下/编译原理/算符优先/SLR.py
[状态栈]:['0']
[符号栈]:['#']
[状态栈]:['0', '3']
[符号栈]:['#', 'i']
[1]: V -> i
[状态栈]:['0', '2']
[符号栈]:['#', 'V']
[状态栈]:['0', '2', '5']
[符号栈]:['#', 'V', '=']
[状态栈]:['0', '2', '5', '10']
[符号栈]:['#', 'V', '=', 'i']
[2]: F -> i
[状态栈]:['0', '2', '5', '8']
[符号栈]:['#', 'V', '=', 'F']
[3]: T -> F
[状态栈]:['0', '2', '5', '7']
[符号栈]:['#', 'V', '=', 'T']
[状态栈]:['0', '2', '5', '7', '13']
[符号栈]:['#', 'V', '=', 'T', '*']
[状态栈]:['0', '2', '5', '7', '13', '9']
[符号栈]:['#', 'V', '=', 'T', '*', '(']
[状态栈]:['0', '2', '5', '7', '13', '9', '10']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'i']
[4]: F -> i
[状态栈]:['0', '2', '5', '7', '13', '9', '8']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'F']
[5]: T -> F
[状态栈]:['0', '2', '5', '7', '13', '9', '7']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'T']
[6]: E -> T
[状态栈]:['0', '2', '5', '7', '13', '9', '15']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E']
[状态栈]:['0', '2', '5', '7', '13', '9', '15', '11']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E', '+']
[状态栈]:['0', '2', '5', '7', '13', '9', '15', '11', '10']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E', '+', 'i']
[7]: F -> i
[状态栈]:['0', '2', '5', '7', '13', '9', '15', '11', '8']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E', '+', 'F']
[8]: T -> F
[状态栈]:['0', '2', '5', '7', '13', '9', '15', '11', '16']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E', '+', 'T']
[9]: E -> E+T
( +, B, C, temp0 )
[状态栈]:['0', '2', '5', '7', '13', '9', '15']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E']
[状态栈]:['0', '2', '5', '7', '13', '9', '15', '20']
[符号栈]:['#', 'V', '=', 'T', '*', '(', 'E', ')']
[10]: F -> (E)
[状态栈]:['0', '2', '5', '7', '13', '18']
[符号栈]:['#', 'V', '=', 'T', '*', 'F']
[11]: T -> T*F
( *, A, temp0, temp1 )
[状态栈]:['0', '2', '5', '7']
[符号栈]:['#', 'V', '=', 'T']
[12]: E -> T
[状态栈]:['0', '2', '5', '6']
[符号栈]:['#', 'V', '=', 'E']
[状态栈]:['0', '2', '5', '6', '11']
[符号栈]:['#', 'V', '=', 'E', '+']
[状态栈]:['0', '2', '5', '6', '11', '10']
[符号栈]:['#', 'V', '=', 'E', '+', 'i']
[13]: F -> i
[状态栈]:['0', '2', '5', '6', '11', '8']
[符号栈]:['#', 'V', '=', 'E', '+', 'F']
[14]: T -> F
[状态栈]:['0', '2', '5', '6', '11', '16']
[符号栈]:['#', 'V', '=', 'E', '+', 'T']
[15]: E -> E+T
( +, temp1, D, temp2 )
[状态栈]:['0', '2', '5', '6']
[符号栈]:['#', 'V', '=', 'E']
[16]: A -> V=E
( =, temp2, ,X )
[状态栈]:['0', '1']
[符号栈]:['#', 'A']
[状态栈]:['0', '1', '4']
[符号栈]:['#', 'A', '#']
True

Process finished with exit code 0

分析过程及四元式产生结果完全正确！

优势

  • 本次代码编写采用了面向对象的编程思想，保证了SLR类的泛用性
  • 只需要改变输入的符号集合及文法规则，即可对不同的满足SLR1文法的语句进行语法分析
  • 程序能给出每一步的精确分析过程，并产生对应四元组

附录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469

class SLR:
    def __init__(self, start, Vn, Vt, rule):
        # 初始化类元素
        self.start = start
        self.Vt = Vt
        self.Vt.append('#')
        self.Vn = Vn
        self.rule = rule
        self.point = '.'
        self.V = Vn + Vt

        # 拓广文法
        self.rule['S'] = start + "#"
        self.Vn.append('S')
        self.start = 'S'

        # 获得first集
        self.first = {vn:set() for vn in self.Vn}
        self.get_first()

        # 获得follow集
        self.follow = {vn: set() for vn in self.Vn}
        self.get_follow()

        # 生成有效项目集
        #self.C = {k : dict() for k in range(12)}
        self.C = {}
        self.tC = [] # 终态项目集
        self.get_C()

        # 生成action表
        self.r = {}  # 记录规约序号，辅助生成action表中的r项
        self.get_r()
        self.action = dict()
        self.get_action()

        # 生成Goto表
        self.goto = dict()
        self.get_goto()

    def get_first(self):
        rule1 = self.rule.copy()
        item = rule1[self.start]
        rule1[self.start] = [item]
        '''
            若X∈Vn 有X→aα , (a ∈Vt )或/和X→ε
            则 a或 /和ε ∈ FIRST(x)
        '''
        for left in rule1.keys():
            for right in rule1[left]:
                if(right[0] in self.Vt):
                    self.first[left].add(right[0])

        '''
           对X→Y1Y2.......Yk(且Y1 ∈Vn), 反复使用以下 直到每一个FIRST(X)不再增大为止.
            i   若Y1 ∈Vn
                则把FIRST(Y1 )\{ε}元素加入FIRST(X)中
            ii  若Y1、Y2、......Y i-1 ∈Vn (2≤i ≤k) 且ε ∈FIRST(Y j) (1≤j ≤i-1)
                则把FIRST(Yi )\{ε}元素加入FIRST(x)中 
            iii 若Y1、Y2、......Yk ∈Vn
                且ε ∈FIRST(Y j) (1≤j ≤k) 则把ε元素加入FIRST(x)中
        '''
        size1 = 0
        size2 = 0
        for key in self.first:
            for item in self.first[key]:
                size1 += len(item)
        while(True):
            for left in rule1.keys():
                for right in rule1[left]:
                    Y1 = right[0]
                    if(Y1 in self.Vn):
                        set1 = self.first[Y1]
                        for item in set1:
                            self.first[left].add(item)

            for key in self.first:
                for item in self.first[key]:
                    size2 += len(item)

            if(size1 != size2):
                size1=size2
                size2=0
                continue
            else:
                break

    def get_follow(self):
        rule1 = self.rule.copy()
        item = rule1[self.start]
        rule1[self.start] = [item]
        # 1. 令# ∈FOLLOW(S) S为文法开始符号
        self.follow[self.start].add('#')

        # 2. 对A→ αBβ, 且β ≠ ε 则将 FIRST(β)\{ε}加入FOLLOW(B)中
        for left in rule1.keys():
            for right in rule1[left]:
                for k in range(len(right)-1):
                    # B:right[k]
                    if(right[k] in self.Vn):
                        # B下一个字符是终结符，则直接加入B的follow集
                        if(right[k+1] in self.Vt):
                            self.follow[right[k]].add(right[k+1])
                        # B下一个字符不是终结符，则将FIRST(β)加入B的follow集
                        elif(right[k+1] in self.Vn):
                            set1 = self.first[right[k+1]]
                            for item in set1:
                                self.follow[right[k]].add(item)

         # 3.反复, 直至每一个FOLLOW(A)不再增大
         # 对A→ αB或A→ αBβ(且ε ∈ FIRST(β))
         # 则FOLLOW(A)中的全部元素加入FOLLOW(B)
        size1=0
        size2=0
        for key in self.follow:
            for item in self.follow[key]:
                size1 += len(item)
        while(True):
            for left in rule1.keys():
                for right in rule1[left]:
                    # B:right[-1] 对A→ αB
                    if(right[-1] in self.Vn):
                        set1 = self.follow[left]
                        for item in set1:
                            self.follow[right[-1]].add(item)

            for key in self.follow:
                for item in self.follow[key]:
                    size2 += len(item)

            if (size1 != size2):
                size1=size2
                size2=0
                continue
            else:
                break

    '''
        开始操作:S为开始符号, S→δ               
        则  S→·δ ∈ C0
    '''
    def op_start(self):
        self.C[0]= {'S':[self.point+self.rule['S']]}

    '''
        闭包操作:closure(Ci)       Ci的闭包        
            ① Ci 的任何项目均属于closure(Ci)        
            ② 若A → α·X β且X∈Vn属于closure(Ci)            
               则X → ·λ 属于closure(Ci)   
               重复,直至 closure(Ci)不再增大.        
            ③ Ci = closure(Ci)
    '''
    def op_closure(self,c_j):
        #closure_i = self.C[i] #dict类型
        closure_i = c_j
        while(True):
            closure_i1=closure_i.copy()
            key_list = list(closure_i.keys())
            for A in key_list:
                for aXb in closure_i[A]:
                    for j in range(len(aXb)-1):
                        if(aXb[j]==self.point and aXb[j+1] in self.Vn):
                            # 如何没有则新建一个key
                            if(aXb[j+1] not in closure_i.keys()):
                                closure_i.update({aXb[j + 1]:[]})
                                key_list.append(aXb[j + 1])
                            for l in rule[aXb[j+1]]:
                                temp = self.point+l
                                if(temp not in closure_i[aXb[j+1]]):
                                    closure_i[aXb[j+1]].append(temp)
            # 重复,直至 closure(Ci)不再增大.
            if(closure_i != closure_i1):
                closure_i1 = closure_i.copy()
            else:
                return closure_i

    '''
        读操作: Go(Ci ,x )     x∈V           
        Go(Ci ,x )=Cj 
        其中: Cj={A→αx·β∣ A→α·x β∈Ci} 
    '''
    def op_go(self,i,x):
        c_j = dict()
        dict_j = self.C[i]

        for A in dict_j.keys():
            for aXb in dict_j[A]:
                for j in range(len(aXb) - 1):
                    if(aXb[j] == self.point and aXb[j+1] == x):
                        if(A not  in c_j.keys()):
                            c_j.update({A:[]})
                        c_j[A].append(aXb[:j]+aXb[j+1]+self.point+aXb[j+2:])
        return c_j

    # 判断C[i]是否为终态
    def judge(self,i):
        dict_i = self.C[i]
        for key in dict_i.keys():
            for value in dict_i[key]:
                if(value[-1]!=self.point):
                    return False
        return True


    def check_in_C(self,closure_j):
        for i in self.C.keys():
            if closure_j == self.C[i]:
                return True
        return False


    def get_C(self):
        # 生成C0={S→ ·δ}
        self.op_start()
        # ∪ {S→ ·δ的闭包操作}
        self.C[0]=self.op_closure(self.C[0])


        '''
        重复以下过程,直至C不再增大为止.          
            Ci读操作,生成Cj1,Cj2,…….Cjn               
            Cj1,Cj2,…….Cjn闭包操作 
            (若其中某项目集已经存在就略去)   
        '''
        i = 0
        j = 1
        while(True):
            # 判断C[i]是否为终态
            if (i == j):
                break
            if(self.judge(i)==True):
                self.tC.append(i)
                i=i+1
                continue
            for v in self.V:
                c_j = self.op_go(i,v)
                if(len(c_j)!=0):
                    #self.C[j] = c_j
                    closure_j = self.op_closure(c_j)
                    flag = True
                    # for key in self.C.keys():
                    #     if(closure_j == self.C[key]):
                    #         flag = False
                    if self.check_in_C(closure_j):
                        flag=False

                    if flag:
                        self.C[j]=closure_j
                        j = j + 1
            if (i<j):
                i=i+1

            else:
                break

    # 用于建分析表的Go函数返回状态集的编号
    def GO(self,i,x):
        c_j = dict()
        dict_j = self.C[i]

        for A in dict_j.keys():
            for aXb in dict_j[A]:
                for j in range(len(aXb) - 1):
                    if (aXb[j] == self.point and aXb[j + 1] == x):
                        if (A not in c_j.keys()):
                            c_j.update({A: []})
                        c_j[A].append(aXb[:j] + aXb[j + 1] + self.point + aXb[j + 2:])
        # 别忘了闭包
        c_j = self.op_closure(c_j)
        for key in self.C.keys():
            if self.C[key]==c_j:
                return key

        return -1

    # 生成辅助规约映射self.r
    def get_r(self):
        rule1 = self.rule.copy()
        item = rule1[self.start]
        rule1[self.start]=[item]
        i = 0
        for left in rule1.keys():
            for right in list(rule1[left]):
                self.r[i] = {left: right}
                i = i+1

    # 构造分析表的action部分
    def get_action(self):
        # 若GO(Ci, a)=Cj  a∈Vt, 置ACTION(i,a)=Sj
        for i in self.C.keys():
            for a in self.Vt:
                j = self.GO(i,a)
                if(j!=-1):
                    self.action[(i,a)]='S'+str(j)

        # 若A→α·∈Ci , 且 a∈FOLLOW(A)
        #  a∈Vt 置ACTION(i,a)=rj (A → α为第 j个产生式)
        for i in self.C:
            for A in self.C[i].keys():
                for item in self.C[i][A]:
                    # 项目最后一个为点 '·'
                    if(item[-1] == self.point):
                        for a in self.follow[A]:
                            # 找到对应的规约产生式
                            for j in self.r.keys():
                                temp = {A:item[:-1]}
                                if(self.r[j] == temp):
                                    self.action[(i,a)]='r'+str(j)


        # 若S→δ·∈ Ck ,(S为拓广文法开始符号）
        # 置ACTION(k,#)=acc
        omiga = rule[self.start]+self.point
        for k in self.C:
            for key in self.C[k].keys():
                if(key==self.start and omiga in self.C[k][key]):
                    self.action[(k,'#')]="acc"


    # 构造分析表的goto部分
    def get_goto(self):
        # 若GO(Ci, A)=Cj  A∈Vn, 置GOTO(i,A)=j
        for i in self.C.keys():
            for A in self.Vn:
                j = self.GO(i, A)
                if (j != -1):
                    self.goto[(i, A)] = j

    # SLR（1）法分析
    # symbol: 符号语句 word: 真实语句
    def compile(self, symbol, word, log):
        # 预定义.PLACE变量
        if log == True:
            E_place = []
            F_place = []
            V_place = []
            T_place = []
            t = 0 #temp计数器
            kk = 1#log计数器

        # 补充#
        symbol+="##"

        # 状态栈
        state = ['0']
        # 符号栈
        charater = ['#']

        #输入串下标
        k=0

        while(True):
            state_now = eval(state[len(state)-1])

            input_ch = symbol[k]

            if ((state_now,input_ch) in self.action.keys()):
                action = self.action[(state_now, input_ch)]
            else:
                action='-1'

            if(action[0]=='S'):
                #if(input_ch != '#'):
                k = k+1
                charater.append(input_ch)
                state.append(action[1:])
                continue

            elif(action[0]=='r'):
                # 规约动作r
                r = {}
                r = self.r[eval(action[1])]
                # 规约长度
                lenth = 0
                # 规约终结符
                substitude = ''
                r_rule=''
                for left in r.keys():
                    substitude = left
                    for right in r[left]:
                        r_rule+=right


                for i in range(len(r_rule)):
                    charater.pop()
                    state.pop()

                # 根据规约规则r_rule决定执行动作, log为分析开关
                if log==True:
                    print("["+str(kk)+"]: "+substitude+" -> "+r_rule)
                    kk = kk+1
                    # ② A →V=E
                    if (substitude == 'A' and r_rule == "V=E"):
                        print("( =, "+E_place.pop()+", ,"+V_place.pop()+" )")

                    # ③ E(1)→E(2)+T
                    elif (substitude == 'E' and r_rule == "E+T"):
                        E1_place = "temp"+str(t)
                        t=t+1
                        print("( +, "+E_place.pop()+", "+T_place.pop()+", "+E1_place+" )")
                        E_place.append(E1_place)

                    # ④ E → T
                    elif (substitude == 'E' and r_rule == "T"):
                        E_place.append(T_place.pop())

                    # ⑤ T(1)→ T(2)*F
                    elif (substitude == 'T' and r_rule == "T*F"):
                        T1_place = "temp"+str(t)
                        t=t+1
                        print("( *, "+T_place.pop()+", "+F_place.pop()+", "+T1_place+" )")
                        T_place.append(T1_place)

                    # ⑥ T → F
                    elif (substitude == 'T' and r_rule == "F"):
                        T_place.append(F_place.pop())

                    # ⑦ F →(E)
                    elif (substitude == 'F' and r_rule == "(E)"):
                        F_place.append(E_place.pop())

                    # ⑧ F → i
                    elif (substitude == 'F' and r_rule == "i"):
                        F_place.append(word[k-1])

                    # ⑨ V →i
                    elif (substitude == 'V' and r_rule == "i"):
                        V_place.append(word[k-1])


                # 新规约终结符进符号栈
                charater.append(substitude)
                new_state = self.goto[(eval(state[len(state)-1]),substitude)]
                state.append(str(new_state))

            elif(action=='acc'):
                return True

            else:
                return False


if __name__ == "__main__":
    # 终结符号集/非终结符号集
    Vn = ['A', 'V', 'E', 'T', 'F']
    Vt = ['+', '-', '*', '/', '(', ')', 'i' , '=']

    # 规则集合
    rule = {
        'A': ["V=E"],
        'E': ["E+T","E-T","T"],
        'T': ["T*F", "T/F", "F"],
        'F': ["(E)","i"],
        'V': ["i"]
    }

    slr = SLR(start='A',Vt=Vt,Vn=Vn,rule=rule)

    test_words = ""
    test_symbol = ""
    f = open("in2.0.txt",'r')
    while(True):
        t = f.readline().strip('\n')
        if(t == ''): break
        test_symbol += t[0]
        test_words += t[-1]

    print(slr.compile(symbol=test_symbol,word=test_words,log=True))
小手一抖⬇️