实验目的
设计和实现最佳置换算法、先进先出置换算法、最近最久未使用置换算法、改进型Clock置换算法、页面缓冲置换算法;通过页面访问序列随机发生器实现对上述算法的测试及性能比较。
前提假设
- 页表用整数数组或结构数组来表示
- 页面访问序列串是一个整数序列,整数的取值范围为0到N-1。页面访问序列串中的每个元素p表示对页面p的一次访问
实验设计
全局变量
为了便于对不同算法的统一设计,在代码中设计了一些全局变量,作如下说明:
| 变量名 | 类型 | 备注 |
|---|---|---|
| req | typedef struct { int request; bool lack=false; int modify=0;} |
记录一个页面请求。 request:请求页号; lack:该请求是否缺页; modify:请求页是否被修改。 |
| re | vector<req> | 数组记录,re[i]代表第i个时刻进来的页面请求结构体。 |
| bar | int [M][N] | 记录物理块情况。 M个块、N个请求。 |
| access | int [M] | 记录M个块所存页号的访问位 |
| modify | int [M] | 记录M个块所存页号的修改位 |
FIFO
FIFO即first in first out
该算法的替换策略为:
每次发生缺页时总是替换出最早进入物理块的页号,即最先进来的就最先出去。
所以整个算法总共分为三步:
页号预装(注:预装页号默认为不会重复,下同)
1
2
3
4
5
6
7
8
9
10
11//没个块,n个请求
double FIFO(int m,int n){
memset(bar, -1, sizeof(bar));
//初始化前0〜m-1个序列
//i: 周期
for(int i=0;i<m;i++){
//j: 块
for(int j=0;j<=i;j++){
bar[j][i] = re[j].request;
}
}检查所到请求是否存在于物理块中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18//装载第i: m〜n-1个序列
for(int i=m;i<n;i++){
//对j:0〜m块,首先把第i-1时段各块的情况拷贝给第i的时段
for(int j=0;j<m;j++){
bar[j][i] = bar[j][i-1];
}
//记录第i个请求
int now_req=re[i].request;
//判断现在内存中有无该请求页号
bool has=false;
for(int j=0;j<m;j++){
if(bar[j][i]==now_req){
has=true;
break;
}
}
//有的话直接下一个
if(has) continue;如果不存在,则将最早进入物理块的页号替换出去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27// 没有的话要考虑把谁替换掉
// 先记录缺页
re[i].lack=true;
// 考察序列范围:第i+1个到第n-1个
// 对m个块中个字各自装载的页号考察
// 需要向前检查bar[j][i],即bar[j]目前内存中的页号装载了几个周期
int long_m=-1;//记录待了最久的bar[j]的次数
int long_j=-1;//记录待了最久的bar[j]的下标j
for(int j=0;j<m;j++){
int temp_m=0;
int temp_no=bar[j][i];
for(int k=i-1;k>0;k--){
if(temp_no==bar[j][k])
temp_m++;
else
break;
}
if(temp_m>long_m){
long_m=temp_m;
long_j=j;
}
}
//替换
bar[long_j][i]=now_req;
}
OPT
最佳页面置换算法OPT,即optimal page replacement
该算法的替换策略为:
选择永不使用或是在最长时间内不再被访问(即距现在最长时间才会被访问)的页面淘汰出内存
所以在遇到缺页时,需要根据物理块中现有的页号向后考察请求队列,将最晚出现或者从未出现的页号替换出内存
整个算法总共分为三步:
页号预装
1
2
3
4
5
6
7
8
9
10
11//最佳置换: m个块,n个周期序列
double OPT(int m,int n){
memset(bar, -1, sizeof(bar));
//初始化前0〜m-1个序列
//i: 周期
for(int i=0;i<m;i++){
//j: 块
for(int j=0;j<=i;j++){
bar[j][i] = re[j].request;
}
}检查所到请求是否存在于物理块中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18//装载第i: m〜n-1个序列
for(int i=m;i<n;i++){
//对j:0〜m块,首先把第i-1时段各块的情况拷贝给第i的时段
for(int j=0;j<m;j++){
bar[j][i] = bar[j][i-1];
}
//记录第i个请求
int now_req=re[i].request;
//判断现在内存中有无该请求页号
bool has=false;
for(int j=0;j<m;j++){
if(bar[j][i]==now_req){
has=true;
break;
}
}
//有的话直接下一个
if(has) continue;如果不存在,则将未来最长时间内不再被请求的页号替换出去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36// 没有的话要考虑把谁替换掉
// 先记录缺页
re[i].lack=true;
// 考察序列范围:第i+1个到第n-1个
// 对m个块中个字各自装载的页号考察
bool find=false;
int far_no=-1,far_m=-1;//记录最远出现的页号和其所在块
for(int j=0;j<m;j++){
int temp_no=bar[j][i];
int temp_m=-1;
int k=i+1;
for(;k<n;k++){
//在未来的请求序列中找到了temp_no
if(re[k].request==temp_no){
temp_m=k;
find=true;
break;
}
}
//记录距离最大的
if(temp_m>far_m){
far_m=temp_m;
far_no=j;
}
//未来请求中没有,则肯定替换这个
if(k==n){
find=false;
bar[j][i]=now_req;
break;
}
}
//找到了一个未来中最大的
if(find){
bar[far_no][i]=now_req;
}
LRU
最近最久未使用置换算法LRU,即Least Recently Used
该算法的替换策略为:
以“最近的过去”作为“最近的将来”的近似,选择最近一段时间最长时间未被访问的页面淘汰出内存
该算法的思想与OPT类似,但搜索方向相反,每次在遇到缺页时其总是根据物理块中现有的页号向前考察请求队列,将最早出现的请求页号替换出内存
整个算法总共分为三步:
页号预装
1
2
3
4
5
6
7
8
9
10double LRU(int m,int n){
memset(bar, -1, sizeof(bar));
//初始化前0〜m-1个序列
//i: 周期
for(int i=0;i<m;i++){
//j: 块
for(int j=0;j<=i;j++){
bar[j][i] = re[j].request;
}
}检查所到请求是否存在于物理块中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18//装载第i: m〜n-1个序列
for(int i=m;i<n;i++){
//对j:0〜m块,首先把第i-1时段各块的情况拷贝给第i的时段
for(int j=0;j<m;j++){
bar[j][i] = bar[j][i-1];
}
//记录第i个请求
int now_req=re[i].request;
//判断现在内存中有无该请求页号
bool has=false;
for(int j=0;j<m;j++){
if(bar[j][i]==now_req){
has=true;
break;
}
}
//有的话直接下一个
if(has) continue;如果不存在,则将此时刻之前最久没有被请求过的页号替换出去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31// 没有的话要考虑把谁替换掉
// 先记录缺页
re[i].lack=true;
// 考察序列范围:第i-1个到第0个
// 对m个块中个字各自装载的页号考察
bool find=false;
int far_no=-1,far_m=0xff;//记录最远出现的页号和其所在块
for(int j=0;j<m;j++){
int temp_no=bar[j][i];
int temp_m=-1;
int k=i-1;
for(;k>0;k--){
//在过去的请求序列中找到了temp_no
if(re[k].request==temp_no){
temp_m=k;
find=true;
break;
}
}
//记录距离最大的
if(temp_m<far_m){
far_m=temp_m;
far_no=j;
}
}
//找到了一个过去中最远出现的
if(find){
bar[far_no][i]=now_req;
}
}
new clock
改进型Clock置换算法与上面三个有所不同,其需要用到页面的访问位和修改位,即在全局变量部分的access和modify数组。
算法的思想如下:
① 从查寻指针当前位置起扫描内存分页循环队列,选择A=0且M=0的第一个页面淘汰;若未找到,转②
② 开始第二轮扫描,选择A=0且M=1的第一个页面淘汰,同时将经过的所有页面访问位置0;若不能找到,转①
所以在算法执行时主要考察两类物理块,即
1类(A =0, M = 0):表示该页面最近既未被访问,又未被修改,是最佳淘汰页。
2类(A =0, M = 1):表示该页面最近未被访问,但已被修改,并不是很好的淘汰页。
算法的设计需要五步:
页号预装、变量初始化
1
2
3
4
5
6
7
8
9
10
11
12
13double new_clock(int m,int n){
memset(bar, -1, sizeof(bar));
//初始化前0〜m-1个序列
//i: 周期
for(int i=0;i<m;i++){
//j: 块
for(int j=0;j<=i;j++){
bar[j][i] = re[j].request;
access[j] = 1;//被访问
modify[j] = re[j].modify;//被修改过
}
}
int p=0;//充当指针检查所到请求是否存在于物理块中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//装载第i: m〜n-1个序列
for(int i=m;i<n;i++){
//对j:0〜m块,首先把第i-1时段各块的情况拷贝给第i的时段
for(int j=0;j<m;j++){
bar[j][i] = bar[j][i-1];
}
//记录第i个请求
int now_req=re[i].request;
int now_modify=re[i].modify;
//判断现在内存中有无该请求页号
bool has=false;
for(int j=0;j<m;j++){
if(bar[p][i]==now_req){
has=true;
access[p]=1;
modify[p]=now_modify;
p = (p+1)%m;
break;
}
p = (p+1)%m;
}
//有的话直接下一个
if(has) continue;如果不存在,则先找第一类 access=0 && modify==0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24// 没有的话要考虑把谁替换掉
// 先记录缺页
re[i].lack=true;
do{
//先找第一类 access=0 && modify==0
bool first=false;
//从指针所指位置开始
for(int j=0;j<m;j++){
if(access[p]==0 && modify[p]==0){
bar[p][i] = now_req;//找到则替换
access[p] = 1;//被访问
modify[p] = now_modify;
p = (p+1)%m;
first=true;
break;
}
p = (p+1)%m;
}
if(first){
break;
}如果第一类不存在,则找第二类 access=0 && modify==1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22//第一类失败
//再第二类 access=0 && modify==1
bool second=false;
for(int j=0;j<m;j++){
if(access[p]==0 && modify[p]==1){
bar[p][i] = now_req;//找到则替换
access[p] = 1;//被访问
modify[p] = now_modify;
p = (p+1)%m;
second=true;
break;
}
else{
access[p]=0;//访问位均改为0
p = (p+1)%m;
}
}
if(second){
break;
}如果第二类也不存在,则转回第三步
1
2
3
4
5
6
7
8//第二类失败
//指针返回开始位置
p=0;
//将所有的访问位复0
for(int j=0;j<m;j++){
access[j]=0;
}
}while(1);
PBA
页面缓冲算法PBA,即Page Buffering Algorithm
该算法与前面提到的四个算法有着很大的差别,简单来说,该算法需要额外创建一个空闲页面链表,该链表的作用好比额外提供了一定数目的空闲物理块,挂在空闲链表上的页号仍然存在于内存中,只是不在现有的驻留集中,即存在位==0。
每当请求页号不在现有的驻留集中时,需要先考察链表上是否挂有请求页号,如果有则将其摘下俩表重新填回驻留集中,如果没有则将填入链首所指向的物理块中。
被替换的页号可以采用上面四种中的任意一种方法决定,在该实验中我选取的替换策略为FIFO。
实现PBA需要额外引入一些新的变量,并且需要重新修改物理块的定义:1
2
3
4
5
6
7
8
9
10
11
12
13
14//PBA:基于先进先出: m个块,n个周期序列,k个空闲块
// 空闲页面链表
typedef struct {
int what;//块内容
int which;//块号
}idle_bar;
list<idle_bar> idle;
// 物理块
typedef struct {
int flag=0;//存在位
int No=-1;//块号
int time=-1;//time时进入块,用于辅助先进先出判断
}NODE;
NODE node[M+K];
算法的设计需要五步:
页号预装、空闲页面链表初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17double PBA(int m,int n,int k){
//初始化前0〜m-1个序列
//i: 周期
printf("预设:\n");
for(int i=0;i<m;i++){
node[i].No=re[i].request;
node[i].flag=1;
node[i].time=i;
}
//idle装入k个空闲物理块
for(int i=0;i<k;i++){
idle_bar temp;
temp.what=-1;
temp.which=m+i;
idle.push_back(temp);
}检查所到请求是否存在于物理块中且在当前驻留集中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//装载第i: m〜n-1个序列
for(int i=m;i<n;i++){
int now_req=re[i].request;
//先在物理块中寻找有没有
int has=-2;
for(int j=0;j<m+k;j++){
//存在位为0,说明是挂在idle上的块
if(node[j].flag==0&&node[j].No==now_req){
//has记录在哪个块中
has=j;
break;
}
if(node[j].flag==1&&node[j].No==now_req){
has=-1;
break;
}
}
//在内存中且在驻留集中
if(has==-1){
printf("[%d]: 在驻留集中\n",now_req);
continue;
}请求存在于物理块中,但不在当前驻留集中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33//在内存中但不在驻留集中
if(has>-1){
printf("[%d]: 在空闲链表上\n",now_req);
//要把其拿回到驻留集中
for(list<idle_bar>::iterator it=idle.begin();it!=idle.end();it++){
if(it->what==now_req){
//fifo替换准则
int mintime=n,minjj=-1;
for(int jj=0;jj<m+k;jj++){
if(node[jj].flag==0)//只能替换存在的
continue;
if(node[jj].time<mintime){
mintime=node[jj].time;
minjj=jj;
}
}
node[minjj].flag=0;
node[has].flag=1;//更新为存在
node[has].time=i;//更新时间
//在链表上删除掉,并把替换下来的minjj放入idle中
idle.erase(it);
idle_bar temp;
temp.what=node[minjj].No;
temp.which=minjj;
idle.push_back(temp);
break;
}
}
for(int ii=0;ii<m+k;ii++)
if(node[ii].flag==1)printf("%d ",node[ii].No);
cout<<endl;
continue;
}请求不在于物理块中,但当前空闲链表中存在空物理块
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42//如果不在物理块(内存)中
if(has==-2){
printf("[%d]: 不在物理块中\n",now_req);
re[i].lack=true;//缺页
//基于fifo替换
int mintime=n,minjj=-1;
for(int jj=0;jj<m+k;jj++){
if(node[jj].flag==0)//只能替换存在的
continue;
if(node[jj].time<mintime){
mintime=node[jj].time;
minjj=jj;
}
}
//决定了要被替换的为node[minjj]
//先看idle中的空闲块没用满的情况
//则新来的直接进空闲块
int flag1=-1;
for(list<idle_bar>::iterator it=idle.begin();it!=idle.end();it++){
//空闲块
if(it->what==-1){
node[it->which].flag=1;
node[it->which].No=now_req;
node[it->which].time=i;
idle.erase(it);//idle链表上删去这个空闲块
idle_bar temp;
temp.what=node[minjj].No;
temp.which=minjj;
idle.push_back(temp);//被替换下来的进idle
node[minjj].flag=0;
flag1=1;
break;
}
}
if(flag1==1){
for(int ii=0;ii<m+k;ii++)
if(node[ii].flag==1)printf("%d ",node[ii].No);
cout<<endl;
continue;//空闲替换成功
}请求不在于物理块中,当前空闲链表中不存在空物理块
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20//idle中已经没有空闲块的情况
//需要替换链首块的内容
//将now_req放入此时idle链首的块里,原来链首的内容被彻底移出内存块
//根据fifo提出新的块放入idle中
int head=idle.begin()->which;
node[head].flag=1;
node[head].time=i;
node[head].No=now_req;
idle.pop_front();//移出队首
idle_bar temp;
temp.what=node[minjj].No;
temp.which=minjj;
idle.push_back(temp);//被替换下来的进idle
node[minjj].flag=0;
for(int ii=0;ii<m+k;ii++)
if(node[ii].flag==1)printf("%d ",node[ii].No);
cout<<endl;
}
在所有页面置换算法实现之后,现在来构建页面访问序列随机生成函数。
随机生成算法
根据实验的要求,符合局部访问特性的随机生成算法执行步骤如下:
- 确定虚拟内存的尺寸N,工作集的起始位置p,工作集中包含的页数e,工作集移动率m(每处理m个页面访问则将起始位置p +1),以及一个范围在0和1之间的值t;
- 生成m个取值范围在p和p + e间的随机数,并记录到页面访问序列串中;
- 生成一个随机数r,0 ≤ r ≤ 1;
- 如果r < t,则为p生成一个新值,否则p = (p + 1) mod N;
- 如果想继续加大页面访问序列串的长度,请返回第2步,否则结束。
根据以上思想,可以编写如下生成函数:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39// 页面访问序列随机生成
/*
虚拟内存大小:16位=64K
工作集的起始位置p,
工作集中包含的页数e,
工作集移动率m(每处理m个页面访问则将起始位置p +1),
以及一个范围在0和1之间的值t;
*/
void init()
{
int p = rand() % 64;
int m = 8, e = 4;
int i, j;
double t;
t = rand() % 10 / 10.0;
for (i = 0; i < 4; i++)
{
//生成m个取值范围在p和p + e间的随机数,并记录到页面访问序列串中;
for (j = i * m; j < (i + 1) *m; j++)
{
req temp;
temp.request = (p + rand() % e) % 64;
temp.modify = rand()%2;//被随机修改,只针对clock算法
re.push_back(temp);
}
//生成一个随机数r,0 ≤ r ≤ 1;
double r = (rand() % 10) / 10.0;
//如果r < t,则为p生成一个新值,否则p = (p + 1) mod N
if (r<t)
{
p=rand()%64;
}
else
{
p=(p+1)%64;
}
}
}
测试
在准备工作都完毕后,这一节将对各个算法进行测试。
注:
1.下列测试均认为预设页面不算做缺页
2.‘X’代表当前请求产生缺页中断
3.应用PBA算法时,既不在驻留集也不在空闲链表上时才认为缺页
生成访问序列
首先调用init()函数,生成符合局部访问特性的随机序列1
2
3序列1:42 44 43 42 42 42 45 43 45 46 46 45 45 43 44 44 46 45 45 44 46 47 44 44 48 47 47 45 45 48 48 45
序列2:54 56 55 55 54 56 57 55 55 56 56 57 56 58 56 56 59 56 57 56 56 56 59 56 59 57 59 59 60 59 58 57
序列3:21 24 22 22 21 23 23 22 23 22 24 24 24 24 24 25 23 26 25 25 24 25 24 24 46 49 48 48 47 47 49 47
下面所有测试均取参数为:1
2m = 3 // 3个物理块
n = 32 // 32个页号请求
FIFO
针对序列1,调用FIFO(m,n),可得到如下执行结果
OPT
针对序列1,调用OPT(m,n),可得到如下执行结果
LRU
针对序列1,调用LRU(m,n),可得到如下执行结果
new clock
针对序列1,调用new_clock(m,n),可得到如下执行结果
PBA
PBA的测试与上述四种略有不同,由于其新增了一个空闲链表,故输出格式采用按时间序列输出。
本次测试采用k=2作为参数,即空闲链表上挂有两个空闲物理块。
针对序列1,调用PBA(m,n,k),可得到如下执行结果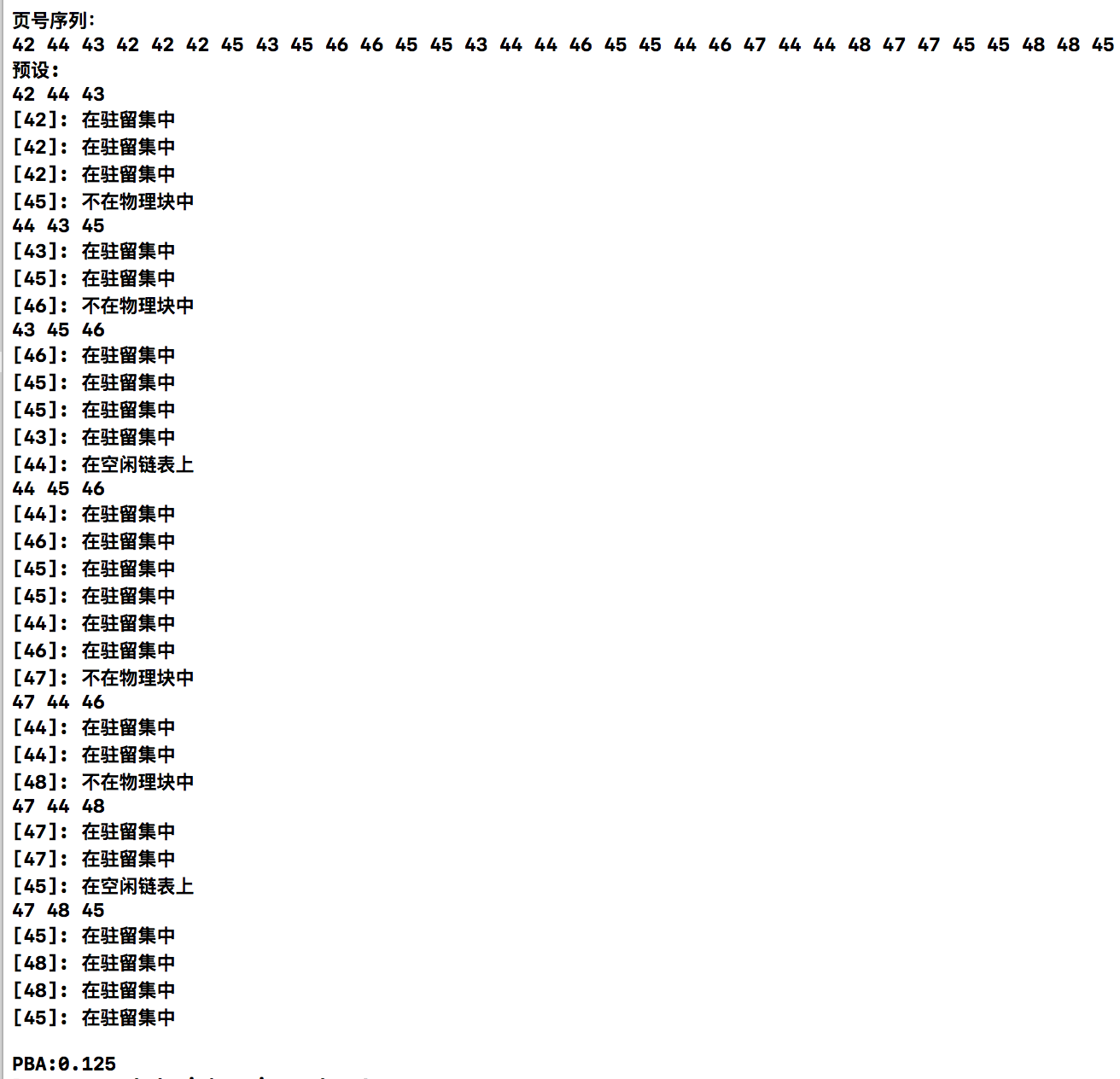
汇总
针对序列2和序列3的测试结果此处不作详细展示
下面对基于序列1、2、3应用五种算法的结果作一个汇总
序列1
| 算法 | 缺页率 |
|---|---|
| FIFO | 0.1875 |
| OPT | 0.15625 |
| LRU | 0.25 |
| new clock | 0.25 |
| PBA | 0.125 |
序列2
| 算法 | 缺页率 |
|---|---|
| FIFO | 0.21875 |
| OPT | 0.15625 |
| LRU | 0.28125 |
| new clock | 0.3125 |
| PBA | 0.125 |
序列3
| 算法 | 缺页率 |
|---|---|
| FIFO | 0.25 |
| OPT | 0.21875 |
| LRU | 0.3125 |
| new clock | 0.375 |
| PBA | 0.21875 |
平均缺页率
| 算法 | 缺页率 |
|---|---|
| FIFO | 0.21875 |
| OPT | 0.17708 |
| LRU | 0.28125 |
| new clock | 0.3125 |
| PBA | 0.15625 |
可以看到,相较之下缺页率最低的页面置换算法为PBA,这也符合实际情况。
另外需要说明的是,在应用new clock算法时,需要人为附加每个请求页的修改位标记,即modify,而另外四种算法则均忽略了修改位,所以单凭该试验结果,并不能说明表现最差的算法为改进型Clock置换算法,只能说明表现较好的算法为PBA和OPT算法。

