编译原理——算符优先语法分析

写在前面

人们常说，对于同一个工程的代码量而言：

C/C++ : JAVA : python = 1000:100:10

前三次在C/C++为主导下创作的作业，代码量明显是一个逐次递增的过程，甚至到实验三的时候，代码量已经破了500大关！
我寻思这可不是一个好的趋势，于是赶紧投笔从戎，放下C刀，从军python

人生苦短，我用python！

目标任务

实验项目

实现算符优先分析算法，完成以下描述算术表达式的算符优先文法的算符优先分析过程。

G[E]:E→E+T∣E-T∣T
     T→T*F∣T/F∣F
     F→(E)∣i

设计说明

终结符号i为用户定义的简单变量,即标识符的定义。

设计要求

（1）构造该算符优先文法的优先关系矩阵或优先函数；
（2）输入串应是词法分析的输出二元式序列，即某算术表达式“专题1”的输出结果。输出为输入串是否为该文法定义的算术表达式的判断结果。
（3）算符优先分析过程应能发现输入串出错。
（4）设计两个测试用例（尽可能完备，正确和出错），并给出测试结果；
（5）考虑编写程序根据算符优先文法构造算符优先关系矩阵，并添加到你的算符优先分析程序中。

实验过程

由于本次实验切换到了python下，虽然python的语法规范宽泛，没有严格的句式要求，但是为了保证结果的泛用性，我决定采用面向对象编程的方法来组织此次作业。

数据结构

在明确好编程思想后，首先需要确定下来的就是如何组织类及类成员，如何存储数据。
下面给出算符优先语法分析类class OPG的成员变量/函数及其设计说明：

成员变量	类型	备注
start	str	记录文法开始符号
Vt	list[str]	记录文法非终结符号集
Vn	list[str]	记录文法终结符号集
rule	dict{str: list[str]}	记录文法产生式
rule1	dict{str: list[str]}	用N替换rule产生式中的非终结符号，辅助判断最左素短语能否被规约
firstVt	dict{str: set()}	记录非终结符号str对应的firstVt集
lastVt	dict{str: set()}	记录非终结符号str对应的lastVt集
matrix	dict{(str,str): str}	记录优先关系矩阵

成员函数	类型	备注
__init__(self,start,Vn,Vt,rule)	class OPG	类的构造函数，通过输入文法的开始符号、非终结符/终结符号集、产生式规则从而构造并返回OPG类
get_firstVt(self)	void	自动生成所有非终结符对应的firstVt集
get_lastVt(self)	void	自动生成所有非终结符对应的lastVt集
get_matrix(self)	void	自动生成优先关系矩阵
get_assistrule(self)	void	生成辅助规则集合rule1
can_statute(self,test)	bool	判断字符串test能否被规约
compile(self,test)	bool	判断输入程序是否满足算符优先文法

自动生成firstVt

生成firstVt由函数get_firstVt(self)实现，算法流程如下：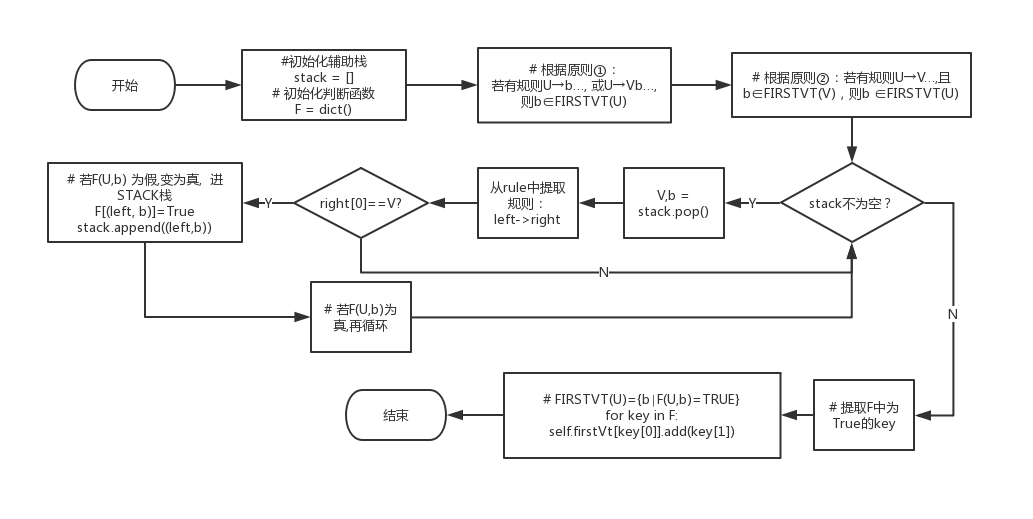

其实现代码如下，注释均详细对应上述流程图

def get_firstVt(self):
    # 初始化firstVt
    self.firstVt = {Vn: set() for Vn in self.Vn}
    # 初始化辅助栈
    stack = []
    # 初始化辅助布尔判断函数
    F = dict()

    # 根据原则①：若有规则U→b…, 或U→Vb…,则b∈FIRSTVT(U)
    # first -> right
    for left in self.firstVt:
        for right in self.rule[left]:
            # U→b…
            if(right[0] in self.Vt):
                self.firstVt[left].add(right[0])
                stack.append((left, right[0]))
                F[(left,right[0])] = True
            # U→Vb…
            elif(len(right)>1 and right[0] in self.Vn and right[1] in self.Vt):
                self.firstVt[left].add(right[1])
                stack.append((left, right[1]))
                F[(left, right[1])] = True

    # 根据原则②：若有规则U→V…,且b ∈FIRSTVT(V)，则b ∈FIRSTVT(U)
    while(len(stack)>0):
        # 弹出栈顶元素,记(V,b)
        V,b = stack.pop()

        for left in self.Vn:
            for right in self.rule[left]:
                # 对每一个形如U→V…的规则
                # U即left
                if(right[0]==V):
                    # 若F(U,b) 为假,变为真,  进STACK栈
                    if((left,b) not in F.keys()):
                        F[(left, b)]=True
                        stack.append((left,b))
                    # 若F(U,b)为真,再循环
                    if(F[(left,b)]==True):
                        continue

    # FIRSTVT(U)={b∣F(U,b)=TRUE}
    for key in F:
        self.firstVt[key[0]].add(key[1])

执行程序的结果如下，可以看出get_firstVt函数已正确执行：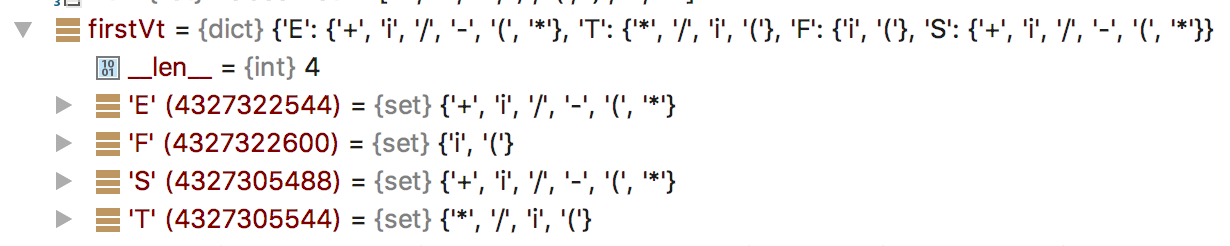

firstVt

自动生成lastVt

生成lastVt由函数get_lastVt(self)实现，流程与生成firstvt几乎相同，只是在规则①和②的地方改为了寻找最后一个或倒数两个字符，算法流程如下：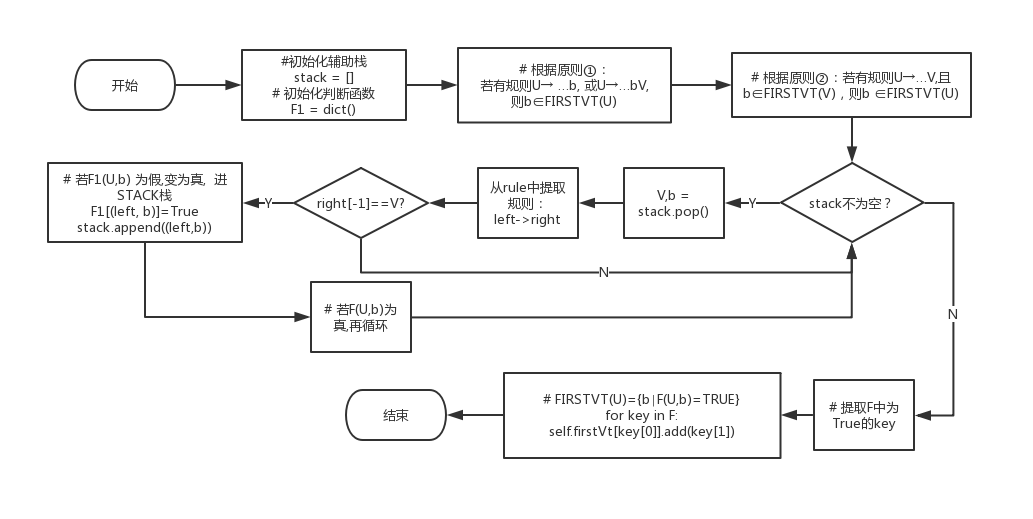

其实现代码如下，注释均详细对应上述流程图

def get_lastVt(self):
# 初始化lastVt
self.lastVt = {Vn: set() for Vn in self.Vn}
# 初始化辅助栈
stack = []
# 初始化辅助布尔判断函数
F1 = dict()

# 根据原则①：若有规则U→…b, 或U→…bV,则b∈LASTVT(U)
# first -> right
for left in self.firstVt:
    for right in self.rule[left]:
        # U→…b
        if(right[-1] in self.Vt):
            self.lastVt[left].add(right[-1])
            stack.append((left, right[-1]))
            F1[(left,right[-1])] = True
        # U→…Vb
        elif(len(right)>1 and right[-1] in self.Vn and right[-2] in self.Vt):
            self.lastVt[left].add(right[-2])
            stack.append((left, right[-2]))
            F1[(left, right[-2])] = True

# 根据原则②：若有规则U→…V,且b ∈ LASTVT(V)，则b ∈ LASTVT(U)
while(len(stack)>0):
    # 弹出栈顶元素,记(V,b)
    V,b = stack.pop()

    for left in self.Vn:
        for right in self.rule[left]:
            # 对每一个形如U→…V的规则
            # U即left
            if(right[-1]==V):
                # 若F(U,b) 为假,变为真,  进STACK栈
                if((left,b) not in F1.keys()):
                    F1[(left, b)]=True
                    stack.append((left,b))
                # 若F(U,b)为真,再循环
                if(F1[(left,b)]==True):
                    continue

# FIRSTVT(U)={b∣F(U,b)=TRUE}
for key in F1:
    self.lastVt[key[0]].add(key[1])

执行程序的结果如下，可以看出get_lastVt函数已正确执行：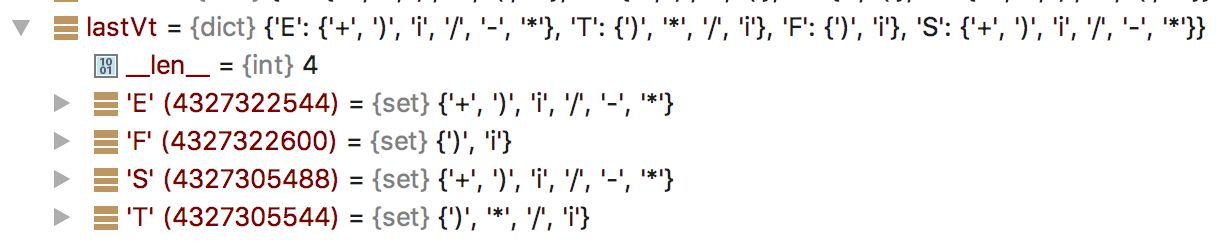

lastVt

自动生成优先关系矩阵

生成优先关系矩阵由函数get_matrix(self)实现，根据算法描述，程序需要考虑以下四种字符组合情况：

• …ab… : Xi = Xi+1
• …aVb… : Xi = Xi+2
• …aU… : a < firstvt(U)
• …Ub… : lastvt(U) > b

对所有产生式中的规则而言，其均满足上述四种情况中的一种，其实现程序如下：

def get_matrix(self):
    # 用字典映射来记录算符优先关系（横，纵）-> '>、<、='
    self.matrix = dict()
    # left -> right
    for left in self.Vn:
        for right in self.rule[left]:
            for i in range(len(right)-1):
                # ...ab... : Xi = Xi+1
                if(right[ i ] in self.Vt and right[i + 1] in self.Vt):
                    self.matrix[(right[i], right[i + 1])] = '='

                # ...aVb... : Xi = Xi+2
                if(i<len(right)-2 and right[i] in self.Vt and right[i+2] in self.Vt):
                    self.matrix[(right[i], right[i + 2])] = '='

                # ...aU... : a < firstvt(U)
                if(right[i] in self.Vt and right[i+1] in self.Vn):
                    for b in self.firstVt[right[i+1]]:
                        self.matrix[(right[i], b)] = '<'

                # ...Ub... : lastvt(U) > b
                if(right[i] in self.Vn and right[i+1] in self.Vt):
                    for a in self.lastVt[right[i]]:
                        self.matrix[(a, right[i+1])] = '>'

    # 处理：'#'
    # '#' < firstvt(S)
    # '#' < lastvt(S)
    # '(#,#)'='='

    for item in self.firstVt[self.start]:
        self.matrix[('#',item)]='<'
    for item in self.lastVt[self.start]:
        self.matrix[(item,'#')]='>'
    self.matrix[('#','#')]='='

最后别忘了对#的处理，由于#只出现在拓广文法S->\#E\#中，所以可以直接应用上述第2、3、4种情况下的对应处理方法，即：

# = #
# < firstVt[E]
lastVt[E] > #

程序的执行结果如下，可以看到优先关系矩阵的详细信息：

优先关系矩阵

判断能否规约

在分析OPG分析过程中，涉及到一步：对于找到的最左素短语，应判断是否存在产生式规则能对其进行规约。
由于在分析过程中，非终结符均被N所替代，所以首先要调用get_assistrule(self)将rule中非的终结符用N来替换，生成辅助规则集rule1，以便检查规约。get_assistrule(self)的代码如下：

def get_assistrule(self):
    self.rule1 = {key : list() for key in self.rule.keys()}
    for key in self.rule.keys():
        for right in self.rule[key]:
            right1=""
            for c in range(len(right)):
                if (right[c] in self.Vn):
                    right1+='N'
                else:
                    right1+=right[c]
            self.rule1[key].append(right1)

在替换完成后，我们便可根据rule1来进行规则的匹配，对于传入的最左素短语test而言，调用函数can_statute(self,test)即可给出判断结果，代码如下：

# 判断最左素短语能否规约
def can_statute(self,test):
    for key in self.rule1:
        for right in self.rule1[key]:
            if(test==right):
                return True
    return False

主分析

在上述准备工作都完成后，接下来便可以开始我们的主分析流程。
主分析对应函数compile(self,test)，其功能为：对于传入的程序串test，可以给出其对于算符优先文法的判别结果，如果出错可以返回出错分析结果。
算法的处理流程如下：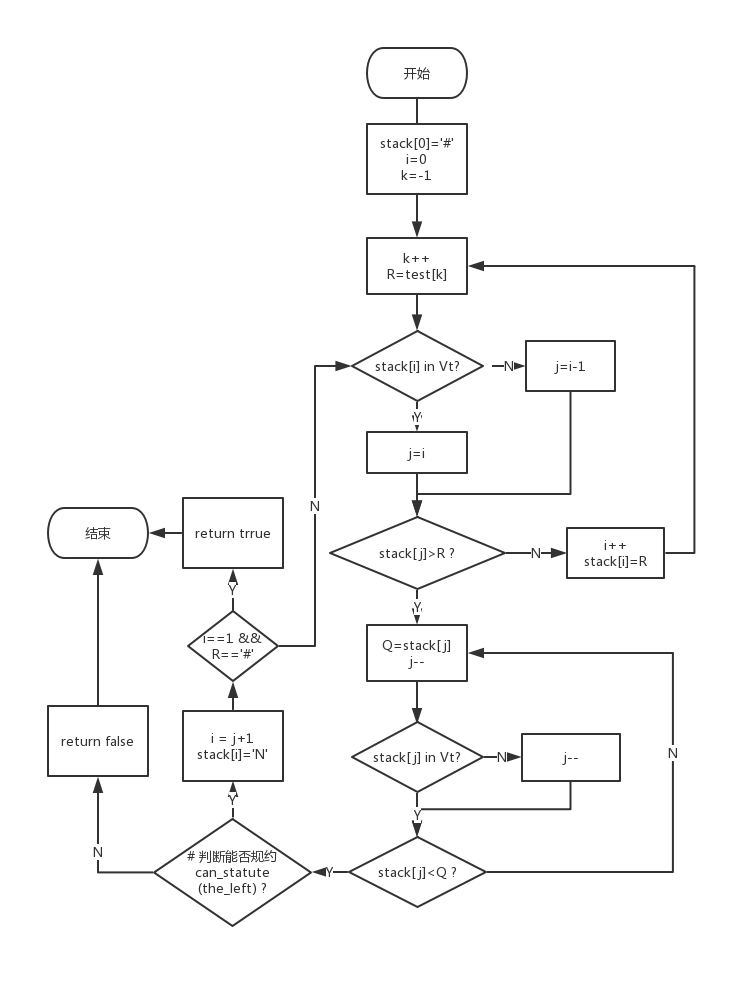

主分析流程

总而言之，分析流程的思想为，先找到一个符号串满足如下约束：
$$
a_j< a_j+1 = a_j+2 = … a_i > R
$$
其中: R为即将输入的字符，a为分析栈中的字符
如果找到了这样的字符串，说明此时我们已经找到了分析栈中待规约的最左素短语$a_j-1…a_i$。
如果其能规约，只需将这一串字符替换为N；如果不能规约，说明其不满足该文法下的算符优先语法，即出错。

主分析的代码如下：

def compile(self,test):
    # 分析栈
    analyse_stack = ['#']

    i = 0
    j = 0 # j+1到i记录最左素短语
    k = -1 # i记录输入串下标

    while(True):
        k = k+1
        # 数组越界则为出错
        if(k>len(test) or i>len(analyse_stack) or j>len(analyse_stack)):
            print("[error] 输入串格式不满足算符文法格式")
            return False
        R = test[k] # R记录输入串下一个要输入的字符

        while(True):
            # 寻找非终结符
            if(analyse_stack[i] in self.Vt):
                j = i
            else:
                j = i-1

            # S(j),R 无优先关系
            if((analyse_stack[j],R) not in self.matrix.keys()):
                print("[error]  \'" + analyse_stack[j] + "\',\'" + R + "\' 无优先关系")
                return False

            # S(j)<R 或 S(j)=R
            if(self.matrix[(analyse_stack[j],R)]!='>'):
                i = i+1
                if(i>=len(analyse_stack)):
                    analyse_stack.append(R)
                else:
                    #analyse_stack.append(R)
                    analyse_stack[i]=R
                break

            # S(j)>R
            while(True):
                # Q=S(j)
                Q = analyse_stack[j]
                j = j-1
                if(analyse_stack[j] not in self.Vt):
                    j = j-1

                # S(j),Q 无优先关系
                if ((analyse_stack[j], Q) not in self.matrix.keys()):
                    print("[error]  \'" + analyse_stack[j] + "\',\'" + Q + "\' 无优先关系")
                    return False
                # S(j)< Q >R
                temp=self.matrix[(analyse_stack[j],Q)]
                if(temp=='<'):
                    break

            # 检验最左素短语是否能规约
            item = j+1
            the_left=""
            while(item<=i):
                the_left += analyse_stack[item]
                item+=1
            if(self.can_statute(the_left)):
                for c in range(j+2,i+1):
                    analyse_stack.pop()
                i = j+1
                analyse_stack[i] = 'N'
            else:
                print("无法规约："+the_left)
                return False

            # 成功
            if(i==1 and R=='#'):
                return True

测试分析

基于题设要求，输入文件为词法分析器的输出结果，类似如下格式：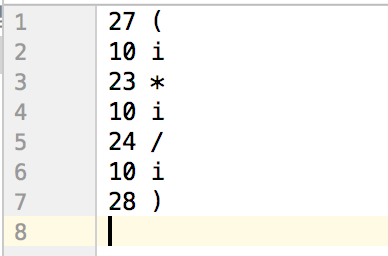

输入文件

我共选用了两组五个测试样例对模型进行了测试，包括两正三负：

正确样例

(i*i/i)

i+(i*i)/i-i

错误样例

模型可检测出不满足产生式的句型：

i++

模型可检测出无优先级的句型：

i+ii-i

模型可检测出包含未定义的符号（即无优先级）的句型：

i=i+i

总结

到此，本次算符优先实验已全部完成。
我的模型具有如下优点：

• 根据产生式规则自动生成firstVt集合
• 根据产生式规则自动生成lastVt集合
• 根据产生式规则自动生成优先关系矩阵
• 可以分析多种出错原因
• 面向对象的思想，模型泛化能力强。只需要改变输入规则集，其可以应对一切算符优先文法。