实验项目
实现LL(1)分析中控制程序(表驱动程序);
完成以下描述赋值语句的LL(1)文法的LL(1)分析过程。1
2
3
4
5
6
7
8
9S→V=E
E→TE′
E′→ATE′|ε
T→FT′
T′→MFT′|ε
F→ (E)|i
A→+|-
M→*|/
V→i
设计说明
终结符号i为用户定义的简单变量,即标识符的定义
设计要求
(1)输入串应是词法分析的输出二元式序列,即某算术表达式“专题1”的输出结果。输出为输入串是否为该文法定义的算术表达式的判断结果;
(2)LL(1)分析过程应能发现输入串出错;
(3)设计两个测试用例(尽可能完备,正确和出错),并给出测试结果;
(4)考虑根据LL(1)文法编写程序构造LL(1)分析表,并添加到你的LL(1)分析程序中。
设计思路
总数据流
LL(1)语法分析器的实现相比递归下降而言复杂了很多,但概括起来程序的实现总共需要如下几步:
- 构造非终结符的First集
- 构造非终结符的Follow集
- 根据First集和Follow集构造LL(1)分析表
- 根据分析表构造分析栈逐个匹配
所以流程如下:
存储结构
在总数据流确定之后,可以发现在分析过程中涉及到很多辅助量,例如各个非终结符对应的First集。
而设置怎样的数据结构来存储这些辅助量是一个在程序编写之前就应该确定下来的问题。
下面给出我在程序编写中所预设的数据结构:
| 变量名 | 类型 | 含义 |
|---|---|---|
| rule | map<string,vector |
记录产生式规则: string→{string,string...} |
| first | map<char,set |
记录各个非终结符号对应的first集 |
| follow | map<char,set |
记录各个非终结符号对应的follow集 |
| Vt | set<char> | 记录终结符集合Vt |
| Vn | set<char> | 记录非终结符集合Vn |
| start | char | 文法开始符号 |
| point | struct Point{char vt; char vn} | 记录分析表坐标 |
| table | map<point,string> | LL(1)分析表:point[坐标]→string[对应动作] |
| file_tuple | typedef struct {int code; char symbol} | 记录输入的二元组,code:编码,symbol:符号 |
| file_text | vector<file_tuple> | 存储整个输入文件 |
在存储结构确定之后,我们便可以着手落实LL(1)语法分析器的实现了,首先从first集的构造开始。
自动构造first集
首先需要对first集有一个理性的定义:
$$
first(α)=\lbrace a| α=^*>aδ,且a∈V_t,δ∈V^* \big\rbrace (若α=^*>ε,则ε∈first(α)\big)
$$
first集的构造有确定的算法,算法的描述如下:
若x∈Vt, 则FIRST(x)={x}
若X∈Vn, 有X→aα,(a∈Vt)或/和X→ε,则a或/和ε∈FIRST(x)
对X→Y1Y2…….Yk(且Y1∈Vn), 反复使用以下直到每一个FIRST(X)不再增大为止.i. 若Y1 ∈Vn,则把FIRST(Y1 )\ {ε}元素加入FIRST(X)中
ii. 若Y1、Y2、……Y i-1 ∈Vn (2≤i ≤k),且ε ∈FIRST(Yj) (1≤j≤i-1),则把FIRST(Yi)\ {ε}元素加入FIRST(x)中
iii. 若Y1、Y2、……Yk ∈Vn,且ε∈FIRST(Yj)(1≤j≤k),则把ε元素加入FIRST(x)中
用代码实现这样抽象的算法并不是一件简约的事情,下面是构造first集的代码,其中各个步骤都标有详细的注释,分别对应上述算法中的各个步骤:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110void make_first(){
//初始化first集
for(set<char>::iterator it = Vn.begin();it!=Vn.end();it++){
set<char>t;
first.insert(make_pair(*it,t));
}
//遍历规则rule
//2.若X∈Vn,有X→aα,(a∈Vt)或/和X→ε 则a或/和ε∈FIRST(x)
for(map<string,vector<string>>::iterator it=rule.begin();it!=rule.end();it++){
//用tempp记录it->first对应的first集
set<char> tempp;
//left -> right
vector<string> right=it->second;
string left=it->first;
for(int i=0;i<right.size();i++){
// X->aα (a∈Vt) a即right[i][0]
if(Vt.count(right[i][0])!=0){
tempp.insert(right[i][0]);
}
// X→ε 则ε∈FIRST(x)
if(right[i]==" "){
tempp.insert(' ');
}
}
if(first.at(*left.c_str()).size()==0){
first.at(*left.c_str())=tempp;
}
else
first.at(*left.c_str()).insert(tempp.begin(),tempp.end());
}
//循环结束条件: 直到每一个FIRST(X)不再增大为止
//3.对X→Y0Y1…….Yk(且Y0 ∈Vn), 反复使用以下直到每一个FIRST(X)不再增大为止
set<char> temp[9];
int k=0,first_size=0;
for(map<string,vector<string>>::iterator it=rule.begin();;it++,k++){
//用temp[k]记录it->first对应的first集
//set<char> temp;
//left -> right
vector<string> right=it->second;
string left=it->first;
//3.对X→Y0Y1…….Yk(且Y0 ∈Vn), 反复使用以下直到每一个FIRST(X)不再增大为止
bool flag=true;//检测连续含{ε}的Yj
for(int i=0;i<right.size();i++){
for(int j=0;j<right[i].size()&&(Vn.count(right[i][j])>0)&&flag;j++){
//FIRST(Yj)
set<char> temp1=first.at(right[i][j]);
//i 若Y0∈Vn 则把FIRST(Y0)\{ε}元素加入FIRST(X)中
if(j==0){
//\{ε}
if(temp1.count(' ')>0){
temp1.erase(' ');
}
//Y0不含{ε}
else{
flag=false;
}
//FIRST(Y0)\{ε}
temp[k].insert(temp1.begin(),temp1.end());
}
/*
ii 若Y1、Y2、……Y i-1 ∈Vn(2≤i ≤k) 且ε ∈FIRST(Y j) (1≤j ≤i-1)
则把FIRST(Yi )\{ε}元素加入FIRST(x)中
*/
else if(j<right[i].size()-1){
//Y0...Yj-1含{ε}
if(temp1.count(' ')>0){
temp1.erase(' ');
}
//Yj不含{ε}
else{
flag=false;
}
//FIRST(Yj)\{ε}
temp[k].insert(temp1.begin(),temp1.end());
}
/*
iii 若Y0、Y1、……Yk ∈Vn且ε ∈FIRST(Yj)(0≤j ≤k)
则把ε元素加入FIRST(x)中
*/
else{
temp[k].insert(' ');
}
}
}
if(first.at(*left.c_str()).size()==0){
first.at(*left.c_str())=temp[k];
}
else
first.at(*left.c_str()).insert(temp[k].begin(),temp[k].end());
//跳出条件
if(k==first.size()-1){
int cnt=0;
//求和,观察first集有无增大
for(int kk=0;kk<=k;kk++){
cnt+=temp[kk].size();
}
//和上一次大小一样,循环终止
if(cnt==first_size)
break;
//重新循环
else{
k=0;
it=rule.begin();
first_size=cnt;
}
}
}
}
自动构造follow集
在构造完first集之后,下一步便可进入到follow集的构造。
当然顺序不是我规定的,但是follow集必须在first集构造完后构造,因为其算法描述是基于first集所定义的。
follow集的定义如下:
$$
follow(A)= \lbrace a| S=^*>αAaδ,且a∈V_t,α,δ∈V^* \rbrace \big(若S=^*>αA,则 \sharp∈follow(A)\big)
$$
当然,也存在构造follow集的成熟算法,算法描述为:
i. 置FIRST(α)={ }
ii. FIRST(X1)\ {ε}加入FIRST(α)
iii. 若ε ∈ FIRST(X1),则FIRST(X2)\ {ε}加入FIRST(α)
若ε ∈ FIRST(X1)且ε ∈ FIRST(X2),则FIRST(X3)\ {ε}加入FIRST(α) ……..以此类推
若ε ∈ FIRST(Xi) 1≤ i ≤n 则ε ∈ FIRST(α)
在定义和算法都描述清晰之后,下一步需要把算法细化为代码实现。
follow集的实现与first集的实现大同小异,代码如下,其中各个步骤都标有详细的注释,分别对应上述算法中的各个步骤:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104void make_follow(){
//初始化follow集
for(set<char>::iterator it = Vn.begin();it!=Vn.end();it++){
set<char>t;
//令#∈FOLLOW(S) S为文法开始符号
if(*it==start)
t.insert('#');
follow.insert(make_pair(*it,t));
}
//遍历规则rule
//2.对A→ αBβ,且β ≠ε, 则将 FIRST(β)\{ε}加入FOLLOW(B)中
for(map<string,vector<string>>::iterator it=rule.begin();it!=rule.end();it++){
//left -> right
vector<string> right=it->second;
string left=it->first;
//对每个left遍历
for(int i=0;i<right.size();i++){
//对left的每一个规则遍历
for(int j=0;j<right[i].size();j++){
//找到B所在:right[i][j]
if(Vn.count(right[i][j])!=0){
set<char> tt;
//β属于Vt
if(Vt.count(right[i][j+1])!=0){
tt.insert(right[i][j+1]);
follow.at(right[i][j]).insert(tt.begin(),tt.end());
}
//β属于Vn,FIRST(β)\{ε}加入FOLLOW(B)中
if(Vn.count(right[i][j+1])!=0){
tt=first.at(right[i][j+1]);
tt.erase(' ');
follow.at(right[i][j]).insert(tt.begin(),tt.end());
}
}//找到B所在:right[i][j]
}//对left的每一个规则遍历
}//对每个left遍历
}//遍历规则rule
// 3.反复, 直至每一个FOLLOW(A)不再增大
// 对A→ αB或A→ αBβ(且ε ∈ FIRST(β))
// 则FOLLOW(A)中的全部元素加入FOLLOW(B)
int k=0;
int follow_size=0;//记录follow集的大小
for(map<string,vector<string>>::iterator it=rule.begin();;it++,k++){
//left -> right
vector<string> right=it->second;
string left=it->first;
//对每个left遍历(一个left对应多个规则)
for(int i=0;i<right.size();i++){
//对left的每一个规则遍历(一个规则对应多个字符)
for(int j=0;j<right[i].size();j++){
//找到B所在:right[i][j]
if(Vn.count(right[i][j])!=0){
set<char> tt;
//到规则的最后一个字符
if(j==right[i].size()-1){
//最后一个字符是Vn,即A→αB,则FOLLOW(A)中的全部元素加入FOLLOW(B)
tt=follow.at(*left.c_str());
follow.at(right[i][j]).insert(tt.begin(),tt.end());
}
//没到最后一个,即A→ αBβ(且ε∈FIRST(β)) 这种情况
else{
bool flag=true;
//检索ε∈FIRST(β)是否成立
for(int jj=j+1;jj<right[i].size()&&flag;jj++){
//right[i][jj]是Vn且包含ε
if(Vn.count(right[i][jj])!=0&&first.at(right[i][jj]).count(' ')!=0){
continue;
}
//right[i][jj]不是Vn或不包含ε
else{
flag=false;
}
}
//A→ αBβ(且ε∈FIRST(β))情况满足
if(flag){
tt=follow.at(*left.c_str());
follow.at(right[i][j]).insert(tt.begin(),tt.end());
}
}
}//找到B所在:right[i][j]
}//对left的每一个规则遍历
}//对每个left遍历
//跳出条件
if(k==follow.size()-1){
int cnt=0;
for(map<char,set<char>>::iterator it1=follow.begin();it1!=follow.end();it1++){
cnt+=it1->second.size();
}
//和上一次大小一样,循环终止
if(cnt==follow_size)
break;
//重新循环
else{
k=0;
it=rule.begin();
follow_size=cnt;
}
}//跳出条件
}
}
自动生成LL(1)分析表
在first集和follow集都构造好之后,我们的前期准备工作已经进入到了最后阶段
现在我们需要做的就是:根据first集和follow集来构造LL(1)分析表
分析表的横坐标由终结符Vt构成,纵轴由非终结符Vn构成,坐标点的内容为对横纵坐标组合所采取的产生式动作。
由每一个产生式A→α1|α2|...|αn确定M[A,a]矩阵,a∈Vt,分析表M的定义如下:
i. 任何a∈FIRST(αi),置M[A, a]=“pop,push(αi′)”,α′为α倒置 或将A→αi 规则填入M[A, a]
ii. 若ε ∈ FIRST(αi),则对于任一个b∈FOLLOW(A),b∈Vt或#,置M[A, b]=“pop”或将A → ε规则填入M[A,b],此时b不属于FIRST(A)
iii. 其它空白为出错
根据分析表的算法描述,可以编写出如下的代码,其中各个步骤都标有详细的注释,分别对应上述算法中的各个步骤:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71void make_table(){
string action;
//纵轴遍历Vn
for(set<char>::iterator it1=Vn.begin();it1!=Vn.end();it1++){
//横轴遍历Vt
for(set<char>::iterator it2=Vt.begin();it2!=Vt.end();it2++){
//结构体t(vn,vt)来记录坐标
point t;
t.vn=*it1;
t.vt=*it2;
action="";
//如果it2是it1的first集元素:it2∈first(it1)
if(first.at(t.vn).count(t.vt)!=0){
//本应有一步动作:查询it2是it1哪一个规则的first集元素
string v= &t.vn;//将it1转化为string类型
vector<string> Trule;
Trule=rule.at(v.substr(0,1));
//剔除空产生式
int T=0;
for(vector<string>::iterator it=Trule.begin();T<Trule.size();it++,T++){
if(*it==" ")
Trule.erase(it);
}
if(Trule.size()>1){
for(int ii=0;ii<Trule.size();ii++){
//空动作不管
if(Trule[ii]==" ")
continue;
//产生式的第一个即为vt,则必定为其first集
if(Trule[ii].find(t.vt)!=string::npos){
action=Trule[ii];
break;
}
}
}
else action = rule.at(v.substr(0,1))[0];//直接拿第一个规则,因为第二个规则即末尾规则肯定为it1->ε
table.insert(make_pair(t, action));
}
//如果it2是it1的follow集元素:it2∈follow(it1),且若ε ∈ FIRST(it1)
else if(first.at(t.vn).count(' ')!=0&&follow.at(t.vn).count(t.vt)!=0){
action="pop";
table.insert(make_pair(t, action));
}
//对应分析表中的空白,即出错
else{
action="-1";
table.insert(make_pair(t, action));
}
}//横轴遍历Vt
//纵轴添加一个‘#’
point t1;
t1.vn=*it1;
t1.vt='#';
//添加条件:Vn->ε 且 ‘#’ ∈ follow(Vn)
if(first.at(t1.vn).count(' ')!=0&&follow.at(t1.vn).count(t1.vt)!=0){
action="pop";
table.insert(make_pair(t1, action));
}
//对应分析表中的空白,即出错
else{
action="-1";
table.insert(make_pair(t1, action));
}
}//纵轴遍历Vn
}
代码中的action变量记录各种情况下应该采取的动作,即M[A,a]
此外,对于空白,算法的描述为错误,代码这里将空白描述为action=‘-1’来代表出错。
到此,我们的first集、follow集和分析表已经全部构造完毕!
构造分析栈
准备工作全部完成之后,接下来便是构造分析栈来对输入二元组进行语法分析。
分析的算法流程描述如下: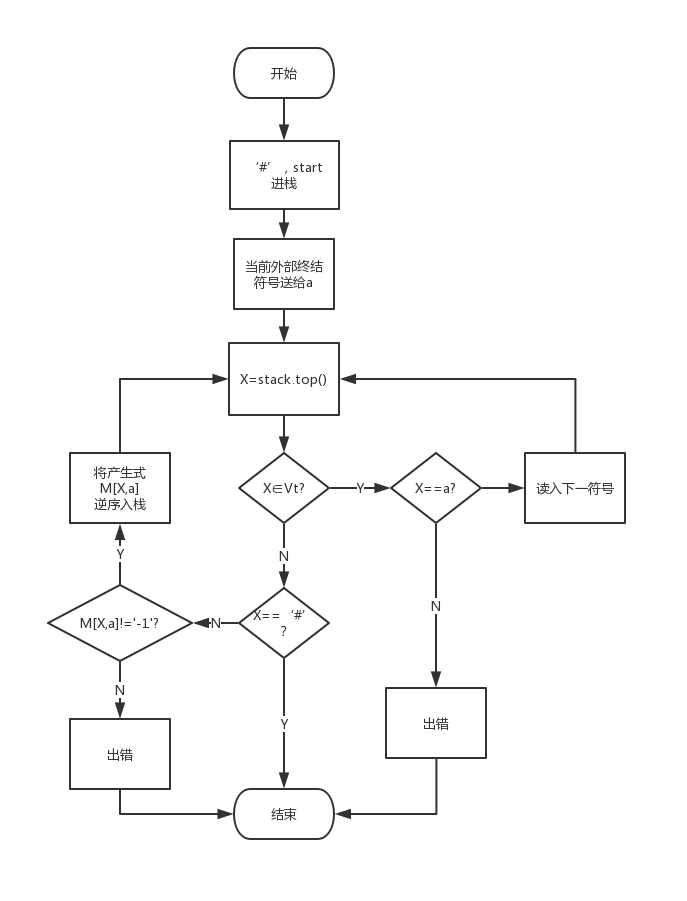
其中start为文法开始符号
测试
选用两组用例包含两错两对,测试结果如下:
正确样例
对于i=i+i,编译结果为: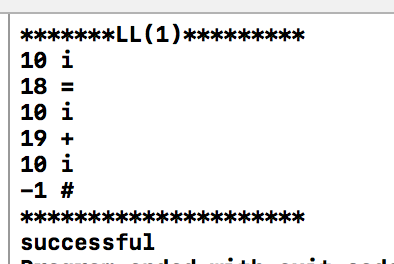
对于i=i*i/i,编译结果为:
错误样例
对于i=i+-,编译结果为:
对于i=i*i/),编译结果为: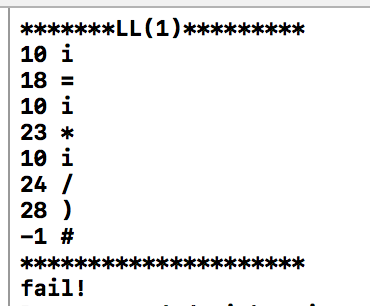
可以看到,语法分析器可以正确实现其功能!
优点
- 通过文件输入规则,自动纳入规则集
- 自动构造first集
- 自动构造follow集
- 自动构造LL(1)分析表
- 通过文件输入二元组,自动输出判别结果
总结
对于这种具有多个复杂存储结构的实验,一定要在事先理清楚各个变量的数据结构的意义,否则很容易陷入迷惑。
此外在c++中需要尽量避免char类型和string类型的混合使用,尽管string提供了c_str方法,但其返回值为char*,在循环时很容易造成指针错误,所以要谨慎使用!

